Question

A coil of one turn is made of a wire of certain length and then from the same length a coil of two turns is made. If the same current is passed in both the cases, then the ratio of the magnetic induction at their centers will be :
A) 2:1
B) 1:4
C) 4:1
D) 1:2

Answer 1

Hint: We will use ampere circuital law which tells us the magnetic field at a given point to solve this question.
Ampere’s circuital law gives the general relation between a current in a wire shape and the magnetic field produced around it.

Complete step-by-step answer:
Let us consider the magnetic induction. The magnetic induction at the center of a current loop is,
$B = \dfrac{{N{\mu _0}I}}{{2\pi R}}$
Where, R is the radius of the loop, N be the number of turns, I is the current .
According to given question, case(1): number of turn N=1and radius of the loop= R
Then, the magnetic field ${B_1} = \dfrac{{{\mu _0}I}}{{2\pi R}}$ ………… (1)
Case (2): the wire of the same length a coil of two turns is made. So, the radius is halved, $R = \dfrac{R}{2}$ and N=2. For both the cases the amount of current passed is the same.
Then, magnetic field ${B_2} = \dfrac{{2{\mu _0}I}}{{2\pi \left( {\dfrac{R}{2}} \right)}}$
${B_2} = 4 \times \left( {\dfrac{{{\mu _0}I}}{{2\pi R}}} \right) = 4{B_1}$
${B_2} = 4{B_1}$
$\dfrac{{{B_1}}}{{{B_2}}} = \dfrac{1}{4}$
Therefore, the correct option is (B) 1:4.

Additional information:Ampere’ circuital law: Ampere’s circuital law gives the general relation between a current in a wire shape and the magnetic field produced around it.
This law is an alternative method to Biot-savart’s law.
The line integral does not depend on the shape of the closed path or on the position of the current carrying wire in the loop. Ampere’s circuital law is applicable for conductors carrying steady current. This law is analogous to gauss law.
Statement: The line integral for a closed curve enclosing an area is equal to ${\mu _0}$ times the net current through the closed bounded area.
$\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}I$
Consider a long straight conductor carrying current I. we have magnetic field B at a point P at a perpendicular distance r from the conductor. The magnetic lines of force are concentric circles centered at the conductor. We choose a circle of radius r as the closed path that is called Amperian loop. The magnitude of B is the same everywhere on the amperian loop. Further, the angle between B and dl is $0^\circ$ everywhere on this path.

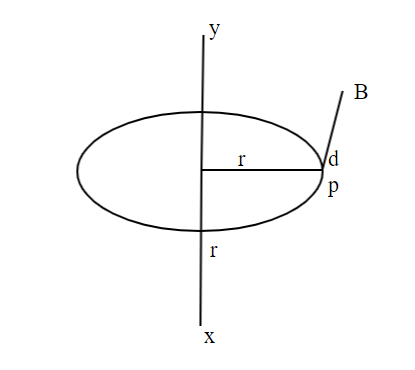
Therefore, applying Ampere’ s circuital law to this closed loop,
$\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}I$ This is a vector form.
In terms of magnitude, we can write it as,
$\oint {Bdl\cos \theta } = {\mu _0}I$
Next step is checking the symmetry.
We have $\theta = 0$, the angle between magnetic field and line element.
$B\oint {dl = {\mu _0}} I$ ………………………… (1)
We know that $\oint {dl = } $ circumference of a circle= $2\pi R$
Where R is the radius of circular path. Now substitute the value of R in equation (1) we get,
$B \times 2\pi R = {\mu _0}I$
$\therefore B = \dfrac{{{\mu _0}I}}{{2\pi R}}$

Note:In this type of question, symmetry is very important. That is, the angle between B and dl at a particular surface should be the same.