Question

A coil of $n$ number of turns is wound tightly in the form of a spiral with inner and outer radii $a$ and $b$, respectively. When a current of strength $I$ is passed through the coil, the magnetic field at its centre is
$A){{\mu }_{0}}nI(b-a){{\log }_{e}}\dfrac{a}{b}$
$B)\dfrac{{{\mu }_{0}}nI}{2ab}$
$C)\dfrac{2{{\mu }_{0}}nI}{b}$
$D)\dfrac{{{\mu }_{0}}nI}{2(b-a)}{{\log }_{e}}\dfrac{b}{a}$

Answer 1

Hint: The idea is to consider a loop element of thickness $dr$, at a distance $r$ from the centre of the spiral. Number of turns per unit length in this loop element is determined. Magnetic field due to this loop element at the centre of the spiral is calculated. Finally, the magnetic field due to the loop element at the centre is integrated from inner radius to outer radius, to get the value of magnetic field at the centre of the coil.
Formula used:
$1)B=\dfrac{{{\mu }_{0}}nI}{2R}$

Complete answer:
We are provided with a coil of $n$ number of turns, tightly wound in the form of a spiral with inner radius $a$ and outer radius $b$. We are required to find the magnetic field at the centre of the coil, when a current of strength $I$ flows through the coil.
For this, let us consider a small loop element of thickness $dr$, at a distance $r$, from the centre of the spiral, as shown in the following figure.

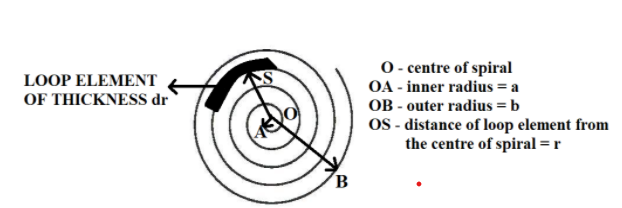
If $T$ represents the number of turns per unit length in the spiral, it is given by
$T=\dfrac{n}{b-a}$
where
$T$ is the number of turns per unit length in the spiral
$n$ is the number of turns in the coil
$b$ is the outer radius of the spiral
$a$ is the inner radius of the spiral
Let this be equation 1.
Now, if $dn$ represents the number of turns per unit length in the loop element $dr$, it is given by
$dn=Tdr=\dfrac{ndr}{b-a}$
where
$dn$ is the number of turns per unit length in the loop element
$dr$ is the thickness of the loop element
$T$ is the number of turns per unit length in the spiral
Let this be equation 2.
When current is allowed to pass through a coil, magnetic field at the centre of the coil is given by
$B=\dfrac{{{\mu }_{0}}nI}{2R}$
where
$B$ is the magnetic field at the centre of the coil
$n$ is the number of turns in the coil
$I$ is the current flowing through the coil
$R$ is the radius of the coil
${{\mu }_{0}}$ is the magnetic constant
Let this be equation 3.
Let us apply this formula to get the magnetic field at the centre of the spiral due to the loop element, we have considered.
If $dB$ is the magnetic field at the centre of the spiral due to the loop element of thickness $dr$, it is given by
$dB=\dfrac{{{\mu }_{0}}I}{2r}dn=\dfrac{{{\mu }_{0}}I}{2r}\left( \dfrac{ndr}{b-a} \right)$
where
$dB$ is the magnetic field at the centre of the spiral due to the loop element
$I$ is the current flowing through the loop element
$r$ is the distance of the loop element from the centre of the spiral
${{\mu }_{0}}$ is the magnetic constant
$b$ is the outer radius of the spiral
$a$ is the inner radius of the spiral
Let this be equation 4.
Now, let us integrate equation 4 to get the magnetic field at the centre of the coil.
Integrating equation 4 from inner radius of the spiral to the outer radius of the spiral, we have
$\int{dB=B}=\int\limits_{a}^{b}{\dfrac{{{\mu }_{0}}I}{2r}\left( \dfrac{ndr}{b-a} \right)}=\dfrac{{{\mu }_{0}}nI}{2(b-a)}\int\limits_{a}^{b}{\left( \dfrac{dr}{r} \right)}=\dfrac{{{\mu }_{0}}nI}{2(b-a)}\left| {{\log }_{e}} \right|_{a}^{b}=\dfrac{{{\mu }_{0}}nI}{2(b-a)}{{\log }_{e}}\left( \dfrac{b}{a} \right)$

Therefore, magnetic field at the centre of the coil is given by
\[B=\dfrac{{{\mu }_{0}}nI}{2(b-a)}{{\log }_{e}}\left( \dfrac{b}{a} \right)\]
where
$B$ is the magnetic field at the centre of the coil (spiral in shape)
$I$ is the current flowing through the coil
${{\mu }_{0}}$ is the magnetic constant
$b$ is the outer radius of the spiral
$a$ is the inner radius of the spiral

Hence, the correct answer is option $D$.

Note:
Students need to be thorough with integration formulas as well as logarithmic expressions. For example, in the above solution, we have used the following integral formula.
$\int{\dfrac{1}{x}dx}={{\log }_{e}}x$
We have also simplified this logarithmic expression as follows.
$\log a-\log b=\log \left( \dfrac{a}{b} \right)$
It is important that students revise such important formulas to solve problems easily.