Question

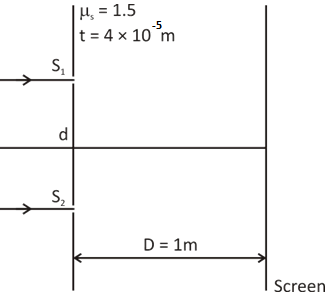
A coherent parallel beam of light of wavelength \[5000\] angstroms is incident normally on the plane of the slits. The slit \[{{\text{S}}_1}\] is covered with a slab of refractive index \[{\mu _{\text{s}}} = 1.5\] and thickness \[t = 4 \times {10^{ - 5}}\,{\text{m}}\] as shown. The separation between the slits is \[d = 1\,{\text{mm}}\] and the separation between the plane of slits and screen is \[D = 1\,{\text{m}}\]. Then the position of the central maxima formed on the screen is:

A. \[1\,{\text{cm}}\] above the point ‘O’.
B. \[2\,{\text{cm}}\] above the point ‘O’.
C. \[1\,{\text{cm}}\] below the point ‘O’.
D. \[2\,{\text{cm}}\] below the point ‘O’.

Answer 1

Hint: First of all, we will find the condition for the central maxima and then find the sine of the angle. Since, the angle is very small, then the sine and the tangent of that angle is equal. After obtaining the tangent of the angle, we will manipulate further to find the position of the central maxima.

Complete step by step answer:
In the given problem, we are supplied with the following data:
The wavelength of the coherent parallel beam of light is \[5000\] angstroms.
The two parallel light rays are incident normally on the plane of the slits which means they are incident at right angles to the plane of the slits.
The slit \[{{\text{S}}_1}\] is covered with a slab of refractive index \[{\mu _{\text{s}}} = 1.5\] .
The thickness of the slab is provided as \[t = 4 \times {10^{ - 5}}\,{\text{m}}\] .
The separation between the slits is \[d = 1\,{\text{mm}}\] .
The separation between the plane of slits and screen is \[D = 1\,{\text{m}}\].
We are asked to find the position of the central maxima formed on the screen.

To begin with, we will need to draw the diagram of the process as described in the question, for better understanding. The two incident rays after refraction through the slit, converge to a point ‘P’.

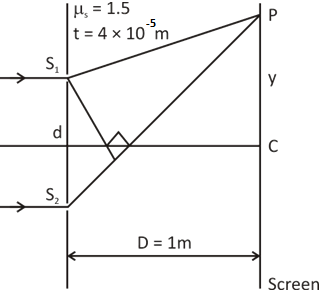
Let us proceed to solve the numerical.
For the condition of central maxima, we have:
\[d\sin \theta = \left( {{\mu _{\text{s}}} - 1} \right)t\] …… (1)
Where,
\[d\] indicates the separation between the slits.
\[\theta \] indicates the angle.
\[{\mu _{\text{s}}}\] indicates the refractive index of the slab.
\[t\] indicates the thickness of the slab.

Now, we substitute the required values in the equation (1), we get:
$d\sin \theta = \left( {{\mu _{\text{s}}} - 1} \right)t \\$
$\Rightarrow 1 \times {10^{ - 3}}\sin \theta = \left( {1.5 - 1} \right) \times 4 \times {10^{ - 5}} \\
\Rightarrow 1 \times {10^{ - 3}}\sin \theta = 0.5 \times 4 \times {10^{ - 5}} \\
\Rightarrow 1 \times {10^{ - 3}}\sin \theta = 2 \times {10^{ - 5}} \\$
Again, we manipulate the above expression:-
$\Rightarrow \sin \theta = \dfrac{{2 \times {{10}^{ - 5}}}}{{1 \times {{10}^{ - 3}}}} \\
\Rightarrow \sin \theta = \dfrac{1}{{50}} \\$
Again, the for the small angle \[\theta \] , we can write:
\[\Rightarrow \tan \theta = \dfrac{1}{{50}}\]
Now, we can write:
\[\Rightarrow \dfrac{y}{D} = \tan \theta \] …… (2)
Where,
\[y\] indicates the position of the central maxima formed on the screen.
\[D\] indicates the distance separating the plane of the slits and the screen.
\[\theta \] indicates the angle.

Now, we substitute the required values in the equation (2) and we get:
\[\Rightarrow \dfrac{y}{D} = \tan \theta \\
\Rightarrow y = D\tan \theta \\
\Rightarrow y = 100\,{\text{cm}} \times \dfrac{1}{{50}} \\
\Rightarrow y = 2\,{\text{cm}} \\
\]
Hence, the central maxima formed on the screen which is \[2\,{\text{cm}}\] above the point ‘O’.

So, the correct answer is “Option B”.

Note:
While solving the problem, we should keep in mind that the point where secondary waves complement each other is called the central limit, resulting in the maximum amplitude at that time.
For a small angle, sine and tangent of that angle is equal.