Question

A Closed loop PQRS carrying a current is placed in a uniform magnetic field. If the magnetic forces on segments PS, SR and RQ are $ {F_1},{F_2} $ and $ {F_3} $ respectively and are in the plane of the paper and along the directions shown, the force on the segment QP is:

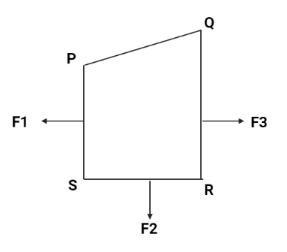
A) $ \sqrt[3]{{{{({F_1} - {F_2})}^2} - F_2^2}} $
B) $ 4{F_3} - {F_1} - {F_2} $
C) $ 5{F_3} - {F_1} - {F_2} $
D) $ \sqrt {{{({F_3} - {F_1})}^2} + F_2^2} $

Answer 1

Hint :The product of current flowing, magnetic field, length of the wire and the angle between the vectors is the magnitude of the force. We see that in this question, the length of the wire is united. Hence, even though forces are applied in all four directions still the net force is zero. Thus, the net force of a current carrying loop in a uniform field is always zero.

Complete Step By Step Answer:
The force on the segment QP is represented as $ {F_4} $ in the figure. Now, we represent $ {F_4} $ in it’s horizontal and vertical components.

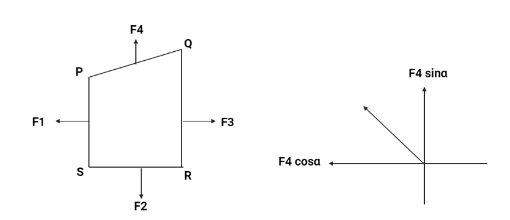
Comparing the forces we get,
 $
  {F_4}\operatorname{Sin} \alpha = {F_2} \\
  {F_4}\operatorname{Cos} \alpha = ({F_3} - {F_1}) \\
  $
Squaring both the equations we get,
 $
  F_4^2{\operatorname{Sin} ^2}\alpha = F_2^2 \\
  F_4^2{\operatorname{Cos} ^2}\alpha = {({F_3} - {F_1})^2} \\
  $
Now, add both the equations
 $
  F_4^2{\operatorname{Sin} ^2}\alpha + F_4^2{\operatorname{Cos} ^2}\alpha = F_2^2 + {({F_3} - {F_1})^2} \\
  F_4^2({\operatorname{Sin} ^2}\alpha + {\operatorname{Cos} ^2}\alpha ) = F_2^2 + {({F_3} - {F_1})^2} \\
  $
Since, $ {\operatorname{Sin} ^2}\alpha + {\operatorname{Cos} ^2}\alpha = 1 $
 $
  F_4^2 = F_2^2 + {({F_3} - {F_1})^2} \\
  {F_4} = \sqrt {F_2^2 + {{({F_3} - {F_1})}^2}} \\
  $
Hence, the correct option is (D).

Note :
The net force of a Closed loop carrying current in a uniform magnetic field will be zero if and only if the magnetic field is perpendicular to the plane of the loop. If it is not perpendicular the net force will be a non-zero value.