Question

A circular ring of radius R and mass m made of a uniform wire of cross-sectional area A is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring. The breaking stress of the material of the ring is $\sigma_b$. Determine the maximum angular speed $\omega_{max}$ at which the ring may be rotated without failure.

A. $\sqrt{\dfrac{\pi A \sigma_{b}}{mR}}$
B. $\sqrt{\dfrac{\pi A \sigma_{b}}{2mR}}$
C. $\sqrt{\dfrac{2\pi A \sigma_{b}}{mR}}$
D. $\sqrt{\dfrac{4\pi A \sigma_{b}}{mR}}$

Answer 1

Hint: Begin by first taking a small component subtended by an angle of the ring. Then, by resolving the net tension experienced by the ring into its radial and tangential components determine which component contributes to the net tension. You should conclude that it is only the radial component.
Then, we know that the centripetal force on the ring by virtue of its angular motion is also directed radially towards the centre of the ring. Thus, equate the equivalent tension and the centripetal force experienced by the ring and rearrange the equation to arrive at the result. Remember to inculcate the breaking stress of the ring into your relation in terms of the tension and the area of the cross section of the material of the ring.
Formula used:
Centripetal force $F_{centripetal} = m\omega^2r$
Breaking stress $\sigma = \dfrac{F}{A}$

Complete answer:
Let us begin by deconstructing the question and establishing an understanding of the same.
We have a circular ring of radius R, mass M, made up of a wire of cross-sectional area A with a breaking stress $\sigma_b$. This ring is rotated about its vertical axis as shown. We have to find the maximum velocity of rotation that the ring can withstand without the wire breaking.

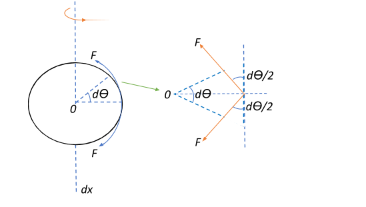
Now, lets us consider a small section of the ring subtended by an angle $d\theta$.
The ring, as a result of rotational motion, experiences a tension F about its circumference.
The net vertical or tangential component of this tension will be 0, since tensions of $Fcos\left(\dfrac{d\theta}{2}\right)$ will act in opposite directions and cancel each other out, as shown in the figure.

Therefore, the tension on the ring comes entirely from the radial (horizontal) components of the tension given by:
$ T_{net} = Fsin\left(\dfrac{d\theta}{2}\right) + Fsin\left(\dfrac{d\theta}{2}\right) = 2Fsin\left(\dfrac{d\theta}{2}\right) \approx 2F\left(\dfrac{d\theta}{2}\right)$ since $d\theta$ is very small.
$\Rightarrow T_{net} = Fd\theta$
Now, let the mass of this small $d\theta$ component of the ring be dm. The length of the arc subtended by this small angle will be $\dfrac{d\theta}{2\pi}$.
Therefore, the mass of the ring over this small component will be: $dm = m\times \dfrac{d\theta}{2\pi}$.
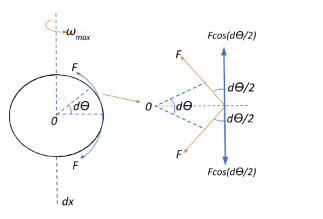
The centripetal force experienced by this component of the ring on rotating it about its vertical axis with the maximum angular velocity $\omega_{max}$ will be:
$F_{centripetal} = (dm)\omega_{max}^2 R = \left(m\times \dfrac{d\theta}{2\pi}\right) \omega_{max}^2 R$
Also, given that the breaking stress of the wire is $\sigma_b $,
$\Rightarrow \sigma_b = \dfrac{F}{A} \Rightarrow F = \sigma_b A$
$\Rightarrow T_{net} = Fd\theta = (\sigma_b A)d\theta$
Now, the centripetal force is nothing but the radial tension of the ring:
$\Rightarrow F_{centripetal} = T_{net}$
$\Rightarrow \left(m\times \dfrac{d\theta}{2\pi}\right) \omega_{max}^2 R =(\sigma_b A)d\theta $
$\Rightarrow \dfrac{m\omega_{max}^2r}{2\pi} = \sigma_b A$
$\Rightarrow \omega_{max}^2 = \dfrac{2\pi\sigma_b A}{mR} \Rightarrow \omega_{max} = \sqrt{\dfrac{2\pi\sigma_b A}{mR} } $

So, the correct answer is “Option C”.

Note:
Remember that it is always helpful to resolve the influencing forces into their components as this will give us a clear picture of which directional forces are contributing to the effects on the system. Failure to do this will result in inconsistent results since we end up accounting for the non-influencing forces or the ones that in fact cancel each other out, like we saw in our problem.

Also remember that the maximum stress a material can stand before it breaks is called the breaking stress. It is also known as the ultimate tensile stress. This is why we had to find the maximum angular velocity that the ring could stand before breaking under the radial forces experienced by the ring.