Question

A circular racing track has inner circumference 336cm and outer circumference 572cm. Find the width of the track.

Answer 1

Hint: This question is based on the formula of circumference of the circle. So, in this question, we will get the inner and outer radius by using the formula. If the radius of the circle is R and the circumference of the circle is C, then we can write, $C=2\pi R$. After getting the inner and the outer radius, for getting the width of the track, we have to subtract the inner radius from the outer radius.

Complete step-by-step answer:
Now, let us assume the inner circumference of the circular track as ${{C}_{1}}$, inner radius as ${{R}_{1}}$, outer circumference of the circular track as ${{C}_{2}}$ and outer radius as ${{R}_{2}}$. So, according to the question, we will get the figure as follows.

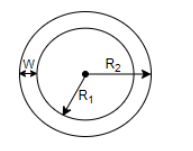
So, from the question, we get,
$\begin{align}
  & {{C}_{1}}=396cm \\
 & {{C}_{2}}=572cm \\
\end{align}$
Let the width of the circular track be W.
So, we know that the width of the track can be found out by subtracting the inner radius from the outer radius. So, we can write it as,
$W={{R}_{2}}-{{R}_{1}}.........(i)$
Now, we have to find the inner and the outer radius of the track. So, for that, we will use the formula of circumference of a circle, that is,
$C=2\pi R$
Where C is the circumference of a circle and R is the radius of that circle.
So, first, we can consider the inner circle of the track, and we have its circumference as 396cm. So, on substituting this value in the formula of the circumference of a circle, we will get,
$\begin{align}
  & {{C}_{1}}=2\pi {{R}_{1}} \\
 & 396=2\pi {{R}_{1}} \\
 & {{R}_{1}}=\dfrac{396}{2\pi } \\
\end{align}$
On taking the value of $\pi =\dfrac{22}{7}$, we get,
$\begin{align}
  & {{R}_{1}}=\dfrac{396}{2\times \dfrac{22}{7}} \\
 & {{R}_{1}}=\dfrac{396\times 7}{2\times 22} \\
 & {{R}_{1}}=63cm.........(ii) \\
\end{align}$
Now, we can consider the outer circle of the track, and we have its circumference as 572cm. So, on substituting this value in the formula of the circumference of a circle, we will get,
$\begin{align}
  & {{C}_{2}}=2\pi {{R}_{2}} \\
 & 572=2\pi {{R}_{2}} \\
 & {{R}_{2}}=\dfrac{572}{2\pi } \\
\end{align}$
On taking the value of $\pi =\dfrac{22}{7}$, we get,
$\begin{align}
  & {{R}_{2}}=\dfrac{572}{2\times \dfrac{22}{7}} \\
 & {{R}_{2}}=\dfrac{572\times 7}{2\times 22} \\
 & {{R}_{2}}=91cm.........(iii) \\
\end{align}$
Now, by substituting the equations (ii) and (iii), in equation (i), we get,
$\begin{align}
  & W={{R}_{2}}-{{R}_{1}} \\
 & W=91-63 \\
 & W=28cm \\
\end{align}$
Therefore, we get the width of the circular track as 28cm.

Note:In this question, students may make mistakes while subtracting as here we are supposed to subtract the inner radius from the outer radius, but they might directly subtract the circumferences, which is wrong. So, this was a simple question, but if we were asked to find the area of the track, then we have to get both radius by using the formula of circumference and then by using the following formula we get the area of the track, $Area=\pi \left( R_{2}^{2}-R_{1}^{2} \right)$.