Question

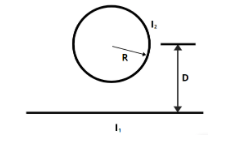
A circular loop of radius $R$ carries current ${I_2}$  in a clockwise direction as shown in figure. The centre of the loop is a distance $D$ above a long straight wire. What are the magnitude and direction of the current ${I_1}$ in the wire if the magnetic field at the centre of loop is zero?

Answer 1

Hint: We can use the Biot-Savart law to find the magnetic field due to a current-carrying loop which is the place at some distance from another current-carrying wire.

Complete step by step solution:
Let us consider that a circular loop of radius $R$
current in the loop is ${I_2}$
direction of current is $clockwise$
the distance between center of loop to the straight wire is $D$,
and magnetic field at the center of the loop is $zero$
At the centre of the circular loop the current ${I_2}$  generates a magnetic field that give by cross \[ \otimes \] . So the current ${I_1}$  must point to the right.
Magnetic field is given by
${B_A} = \dfrac{{{\mu _o}{I_2}}}{{2R}}$ …………...( 1)
And
${B_B} = \dfrac{{{\mu _o}{I_1}}}{{2\pi D}}$ ………...( 2)
Comparing both magnetic field equations, we get
\[\dfrac{{{\mu _o}{I_2}}}{{2R}} = \dfrac{{{\mu _o}{I_1}}}{{2\pi D}}\]
For complete cancellation the two fields’ magnitude, we get
${I_1} = \dfrac{{\pi D{I_2}}}{R}$

Hence, The magnitude of the current ${I_1}$ in the wire is ${I_1} = \dfrac{{\pi D{I_2}}}{R}$ and the direction of the current in the straight wire is left to right when current flowing in the wire is clockwise and magnetic field at center is zero.

Note:When the current is straight which means the current is passing through a straight wire. The magnetic field produced due to current through a straight conductor is in the form of a concentric circle.