Question

A circular cylinder of height \[{{h}_{0}}=10cm\] and radius \[{{r}_{0}}=2cm\] is opened at the top and filled with liquid. It is rotated about its vertical axis. Determine the speed of rotation so that half the area of the bottom gets opposed (\[g=10m{{s}^{-2}}\])

Answer 1

Hint: We need to find the angular velocity at which the container is rotated so as a minimum condition is attained. We can substitute the given condition in Bernoulli's principle and find the required solution of angular velocity directly from it.

Complete answer:
We are to find the angular velocity at which the cylindrical container is rotated so that the liquid filled in the bottom of the container initially now moves up emptying half the bottom. In order to find this, we need to find the radius involved in this area. After finding the area, we need to use Bernoulli's theorem to get the velocity involved.
Let us consider the situation. A cylinder of circular base is filled with liquid. It is rotated along its vertex as shown below.

       

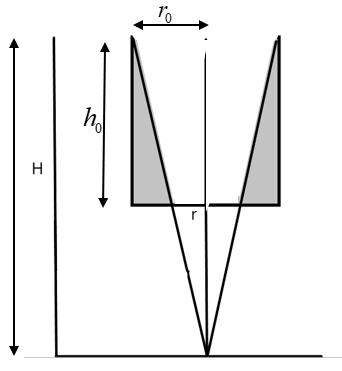
The situation demands that the area of the bottom which is exposed is half its total area. So, we can find the radius, ‘r’ of the bottom area that is exposed as –
\[\begin{align}
  & \text{Area of the bottom, A}=\pi {{r}_{0}}^{2} \\
 & \text{Area of the bottom exposed, A }\!\!'\!\!\text{ }=\dfrac{1}{2}A=\pi {{(\dfrac{{{r}_{0}}}{\sqrt{2}})}^{2}} \\
 & \Rightarrow \text{ }r=\dfrac{{{r}_{0}}}{\sqrt{2}} \\
\end{align}\]
Now, let us consider the Bernoulli’s theorem, given as –
\[{{P}_{1}}+\rho g{{h}_{1}}+\dfrac{1}{2}\rho {{v}_{1}}^{2}={{P}_{2}}+\rho g{{h}_{2}}+\dfrac{1}{2}\rho {{v}_{2}}^{2}\]
The pressure \[{{P}_{1}}\text{ and }{{P}_{2}}\]are the atmospheric pressure since the cylinder is assumed to be open.
We can substitute the heights from the figure as –
\[\begin{align}
  & {{h}_{1}}=H,\text{ } \\
 & {{h}_{2}}=H-{{h}_{0}} \\
\end{align}\]
Now we need to find the velocities \[{{v}_{1}}\text{ and }{{v}_{2}}\], which are used to find the angular velocities.
Substituting the known parameters, we get –
\[\begin{align}
  & P+\rho gH+\dfrac{1}{2}\rho {{v}_{1}}^{2}=P+\rho g(H-{{h}_{0}})+\dfrac{1}{2}\rho {{v}_{2}}^{2} \\
 & \Rightarrow \text{ }\dfrac{1}{2}\rho ({{v}_{2}}^{2}-{{v}_{1}}^{2})=\rho g{{h}_{0}} \\
 & \Rightarrow \text{ }{{v}_{2}}^{2}-{{v}_{1}}^{2}=2g{{h}_{0}}\text{ --(1)} \\
\end{align}\]
Now, we know the relation of radius with that of the angular velocity as –
\[\omega =\dfrac{v}{r}\]
Now, we know that the angular velocity remains constant independent of the radius. So, we can substitute in (1) as –
\[\begin{align}
  & \Rightarrow \text{ (}\omega {{\text{r}}_{0}}{{\text{)}}^{2}}-{{(\omega r)}^{2}}=2g{{h}_{0}}\text{ } \\
 & \Rightarrow \text{ }{{\omega }^{2}}=\dfrac{2g{{h}_{0}}}{{{r}_{0}}^{2}-{{r}^{2}}} \\
 & \text{but,} \\
 & \text{ }r=\dfrac{{{r}_{0}}}{\sqrt{2}} \\
 & \Rightarrow \text{ }\omega =\sqrt{\dfrac{4g{{h}_{0}}}{{{r}_{0}}^{2}}}=2\dfrac{\sqrt{g{{h}_{0}}}}{{{r}_{0}}} \\
 & \Rightarrow \text{ }\omega =\dfrac{2\times \sqrt{10\times 10\times {{10}^{-2}}}}{2\times {{10}^{-2}}}=100rad{{s}^{-1}} \\
\end{align}\]
The required solution is \[\omega =100rad{{s}^{-1}}\], the angular velocity of the rotation of the cylinder.

Note:
The angular velocity remains constant when the given condition, that the half the area of the bottom is exposed, is maintained throughout. We have to keep this in mind while computing the steps to reach the angular velocity from the height and radius of the cylinder.