Question

A circular coil of radius $10cm$, 500 turns and resistance $2\Omega $ is placed with its plane perpendicular to the horizontal component of the earth's magnetic field. It is rotated about its vertical diameter through ${180^ \circ }$m in 0.25 s. What is the current induced in the coil?
(Horizontal component of the earth’s magnetic field at that place is $3.0 \times {10^{ - 5}}T$)
A. $1.9 \times {10^{ - 3}}A$
B. $2.9 \times {10^{ - 3}}A$
C. $3.9 \times {10^{ - 3}}A$
D. $4.9 \times {10^{ - 3}}A$

Answer 1

Hint: Change in Magnetic flux linked with the coil leads to induced voltage or emf. It is given by Faraday’s law of induced emf $\varepsilon = - N\dfrac{{d\phi }}{{dt}}$ where N is number of turns of coil, $\phi $ is magnetic flux and $\varepsilon $ is induced emf.

Formula Used:
1. Faraday’s law of induced emf, $\varepsilon = - N\dfrac{{d\phi }}{{dt}}$ …… (a)
2. Magnetic flux, \[\phi = B.A = BA\cos \theta \] …… (b)
3. Ohm’s Law, $I = \dfrac{\varepsilon }{R}$ …… (c)

Complete step by step answer:
Given,
Number of turns, $N = 500$
Magnetic field perpendicular to cross section area, ${B_H} = 3 \times {10^{ - 5}}T$
Resistance present in the coil, $R = 2\Omega $
Total time taken to rotate between initial and final position, $\Delta t = 0.25s$
Total angle rotated, $\Delta \theta = {180^ \circ }$

Diagram:
Given below schematic diagram depicting the situation:

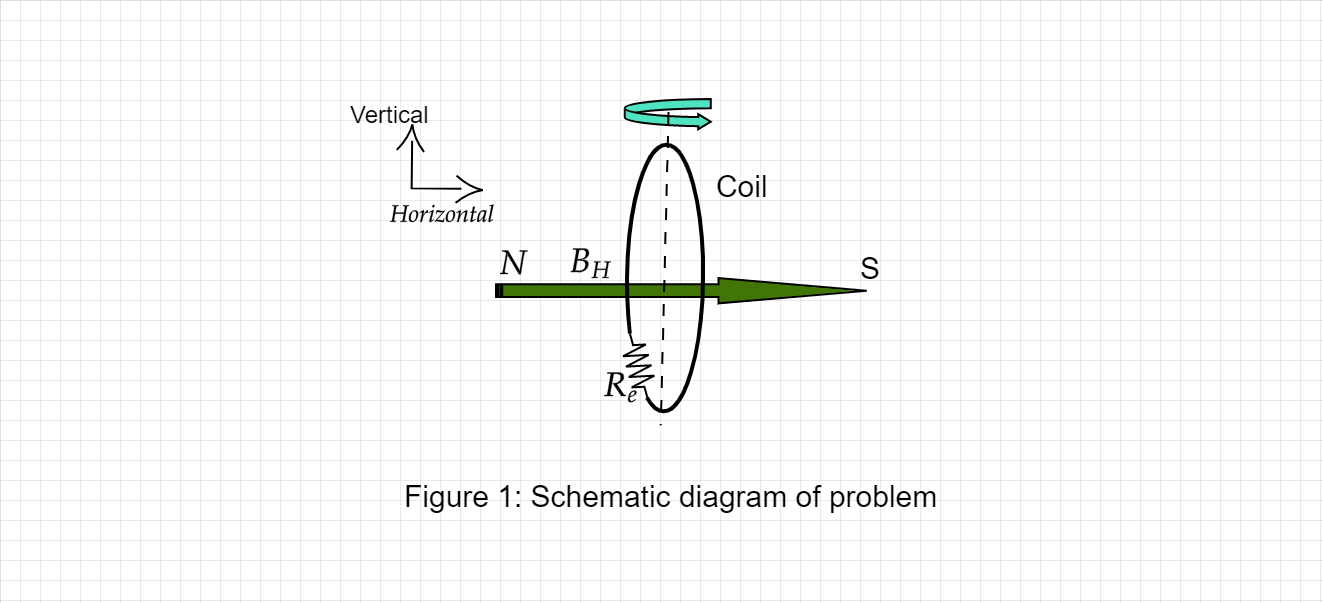
Step 1 of 6:

Initially, plane of the coil is perpendicular to ${B_H}$
Substituting values in equation (b) gives Initial magnetic flux ${\phi _i} = {B_H}.A\cos 0$ as angle between normal of plane and field is 0
$ \Rightarrow {\phi _i} = {B_H}A$ …… (1)

Step 2 of 6:

Finally, plane of the coil is again perpendicular to ${B_H}$ but antiparallel
Substituting values in equation (b) gives Final magnetic flux ${\phi _f} = {B_H}.A\cos (180)$
$ \Rightarrow {\phi _f} = - {B_H}A$ …… (2)

Step 3 of 6:

Change in magnetic flux =$\Delta \phi = {\phi _f} - {\phi _i}$
$ \Rightarrow \Delta \phi = - {B_H}A - {B_H}A = - 2{B_H}A$ …… (3)

Step 4 of 6:
Induced emf in the coil due to change in magnetic flux given by equation (a), $\varepsilon = - N\dfrac{{d\phi }}{{dt}} = - N\dfrac{{\Delta \phi }}{{\Delta t}}$ for finite time and finite angle rotation approximation.

Substituting values from equation (3) in equation (a) we get
$\varepsilon = - N\dfrac{{\Delta \phi }}{{\Delta t}} = - 500\dfrac{{ - 2{B_H}A}}{{\Delta t}}$ …… (4)

Step 5 of 6:

Putting values of variables in equation (4) from the given values we get

$\varepsilon = 500 \times \dfrac{{2 \times 3\pi \times {{10}^{ - 7}}}}{{0.25}} = 0.00038V$ …… (5)
Step 6 of 6:

Substituting value from equation (5) in equation (C) with value of resistance we get
\[I = \dfrac{\varepsilon }{R} = \dfrac{{0.00038}}{2}A\]
\[ \Rightarrow I = 1.9 \times {10^{ - 3}}A\]

Correct Answer:
A. $1.9 \times {10^{ - 3}}A$

Note: Here we used discrete time approximation of Faraday’s law because we have been given discrete values of time and flux change. Otherwise, we need to differentiate time varying magnetic flux linkage with the coil.