Question

A circuit consisting of five resistors each of resistance R, forming a Wheatstone bridge. What is the equivalent resistance of the circuit?
 \[\begin{align}
  & \text{A) 2R} \\
 & \text{B) R} \\
 & \text{C) }\dfrac{2R}{3} \\
 & \text{D) }\dfrac{R}{2} \\
\end{align}\]

Answer 1

Hint: We can check the Wheatstone’s bridge condition for the given situation and evaluate the resistances accordingly. If the circuit turns out to be in accordance with the Wheatstone’s condition, then we can easily calculate the effective resistance of the circuit.

Complete step by step answer:
Wheatstone’s bridge condition is a special condition which relates the resistances in the given circuit. It says that if in a series-parallel circuit, if the opposite resistances are in a constant ratio, then the node joining them will be an equipotential point and hence, avoids any current through the middle resistance.

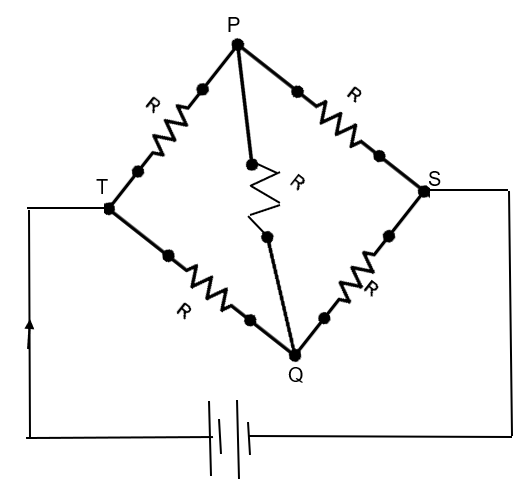
In the above figure, all the resistors of resistance R are connected such that they are in a series-parallel connection.
Now, let us find the ratio of the resistances on opposite arms, which turns out to be as –
\[\dfrac{R}{R}=\dfrac{R}{R}=1\]
This is the condition for Wheatstone’s bridge condition. The ratio between the resistances of the resistors in the opposite arms is equal.
Thus, we have concluded that the given resistance network follows the Wheatstones’s bridge condition. As a result, we know that the current passing through the middle of the circuit joining the equipotential points P and Q is null.
This results in the formation of a simple circuit as shown below –

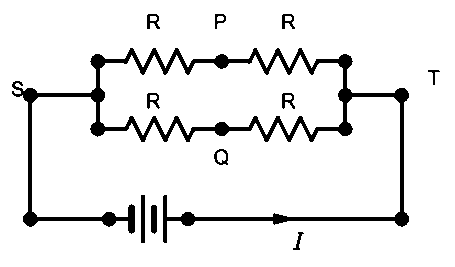
Now, we can easily calculate the equivalent resistance of the network as –
\[\begin{align}
  & {{R}_{s1}}=R+R=2R \\
 & \text{and,} \\
 & {{R}_{s2}}=R+R=2R \\
\end{align}\]
The series resistances are in parallel to each other and thus, the equivalent resistance becomes,
\[\begin{align}
  & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{s1}}}+\dfrac{1}{{{R}_{s2}}} \\
 & \Rightarrow \text{ }{{R}_{eq}}=\dfrac{{{R}_{s1}}{{R}_{s2}}}{{{R}_{s1}}+{{R}_{s2}}} \\
 & \Rightarrow \text{ }{{R}_{eq}}=\dfrac{2R.2R}{2R+2R} \\
 & \therefore \text{ }{{R}_{eq}}=R \\
\end{align}\]
The equivalent resistance of the network is, therefore, R.
The correct answer is option B.

Note:
The Wheatstone’s bridge condition is the underlying property for many electrical applications. The Meter bridge and the potentiometer are the major equipment which use the balancing condition of Wheatstone’s bridge. The connection to the galvanometer is the null resistance in the case.