Question

A circle is inscribed in a regular hexagon of side \[2\sqrt 3 \]cm. Find the circumference of the inscribed circle.

Answer 1

Hint: The circumference of the circle \[P = 2\pi r\]
In this question where a circle is inscribed in a regular hexagon we know the central angle of a hexagon \[ = {60^ \circ }\], so we will find the other angles of the triangle and then we will find the radius of the circle which will be equal to the sides of the triangle and by using this radius we will find the circumference of the circle.

Complete step-by-step answer:
Side of the regular hexagon\[a = 2\sqrt 3 cm\]
Now since a regular hexagon has 6 sides, hence we can say the central angle of a hexagon \[ = \dfrac{{{{360}^ \circ }}}{6} = {60^ \circ }\]

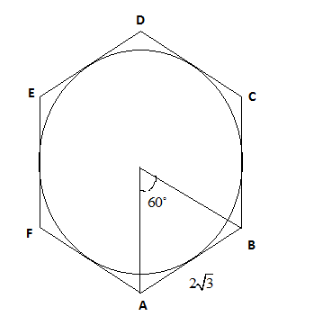
Now from the figure we can say \[\angle AOB = {60^ \circ }\](Central angle of regular hexagon is \[ = {60^ \circ }\])
Now in the \[\Delta AOB\]
 Since the total sum of the angles of a triangle is equal to \[{180^ \circ }\], hence we can write
\[\angle AOB + \angle OAB + \angle OBA = {180^ \circ }\]
Now since\[\angle AOB = {60^ \circ }\], so we can write
\[
  \angle OAB + \angle OBA = {180^ \circ } - {60^ \circ } \\
   = {120^ \circ } \;
 \]
Therefore \[\angle AOB = \angle OAB = \angle OBA = {60^ \circ }\]
Now since all the angles of the triangle are equal hence we can say the triangle is an equilateral triangle, so all the sides of the triangle will also be equal
\[\therefore AO = BO = AB = 2\sqrt 3 cm\]
Now this length \[2\sqrt 3 cm\]will be the circum-radius of the circle which is inscribed in a regular hexagon
\[r = 2\sqrt 3 cm\]
We know the Perimeter of a circle is given by the formula
\[P = 2\pi r\]
Hence by substituting the value of the radius of the circle, we get
\[
  P = 2\pi \times 2\sqrt 3 \\
   = 4\pi \sqrt 3 cm \;
 \]
Therefore the circumference of the inscribed circle \[ = 4\pi \sqrt 3 cm\]

Note: Students must note that there are six equilateral triangles in a hexagon so we can say the sides of the hexagon will also be equal to the radius of the hexagon.