Question

A circle is inscribed in a regular hexagon of side $2\sqrt 3 cm$ . Find the circumference of the inscribed circle.

Answer 1

Hint:To solve this problem we should know about concept of circumscribed as well as basic trigonometry
Circumscribed: Circumscribed of a polygon is a circle that passes through all the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
A trigonometric property, $\cot \theta = \dfrac{{base}}{{perpendicular}}$

Complete step by step answer:
As given in question we will draw diagram,

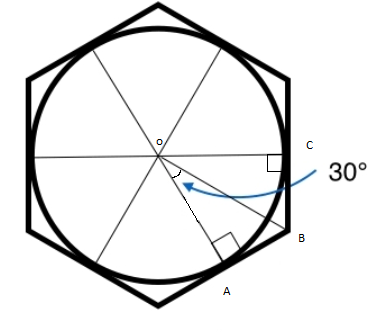
It is obvious from figure that
Let, there are two triangle AOB and COB,
In, $\Delta $ AOB and $\Delta $ BOC. We have,
 $AO = CO$ (radius of circle)
And $OB$ is common if hypotenuse is equal.
So, by RHS criteria both triangles are congruent.
Hence, $\angle AOB = \angle BOC$
And \[\angle AOC = {60^ \circ }\] (circle are divided in six parts)
So, $\angle AOB = \angle BOC = {30^ \circ }$
In, $\Delta $ AOB:
 $\cot \,{30^ \circ } = \dfrac{{base}}{{perpendicular}}$
As, length of the side of the hexagon is $2\sqrt 3 cm$ . so, $AB = \sqrt 3 cm$ .
So,
$\dfrac{{Radius\,of\,the\,circle}}{{half\,the\,side\,of\,hexgon}} = \cot \,{30^ \circ }$
 $ \Rightarrow \dfrac{{Radius\,of\,the\,circle}}{{\dfrac{1}{2} \times 2\sqrt 3 }} = \sqrt 3 $
(As $\cot \,{30^ \circ } = \sqrt 3 $ )
 $ \Rightarrow Radius\,of\,the\,circle(r) = 3cm$
So circumference of the inscribed circle $ = 2\pi r = 2\pi \times 3 = 6\pi $

Note: properties of regular hexagon:
It has six sides and six angles and the measurements of all angles are equal.
The total number of diagonals in a regular hexagon is nine.
The sum of all interior angles is equal to ${720^ \circ }$ .