Question

A circle is circumscribed about a trapezoid. Prove that this is possible If and only if the trapezoid is isosceles.

Answer 1

Hint: Trapezoid: A flat shape with \[4\] straight sides that has a pair of opposite sides parallel.
Circumscribed: Circumscribed of a polygon is a circle that passes through all the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.

Complete step by step solution:
Let ABCD be an isosceles trapezoid with the bases AB and CD and the lateral sides AD and BC.

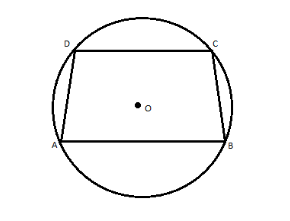
Here, we need to prove that there is a circle which passes through all the vertices of the trapezoid A, B, C and D. So, the circle circumscribed about a trapezoid is isosceles.
Let us draw the diagonals of the trapezoid AC and BD and consider the triangles $\Delta $ ABC and $\Delta $ ABD.

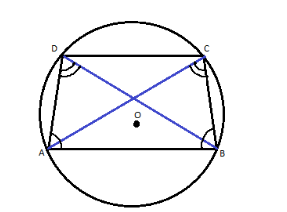
These triangles have the common side AB and the congruent sides BC and AD (the latest is because the trapezoid ABCD is isosceles).
The angles BAD and ABC concluded between these congruent sides are congruent as the base angles of the isosceles trapezoid.
Hence, the triangles $\Delta $ ABC and $\Delta $ ABD are congruent in accordance with the SAS- test for the triangles congruence.
It implies that the angles ABC and ABD are congruent as the corresponding angles of congruent triangles.
Thus the angles ABC and ABD are congruent and leaning on the same segment AB. Hence, these angles are inscribed in a circle.
The converse statement is true that if the trapezoid is inscribed in a circle, then the trapezoid is isosceles.
From the above, By combining the direct and the converse statements you can conclude that a trapezoid can be inscribed in a circle if and only if the trapezoid is isosceles.

Note: Property of trapezoid:
The legs are congruent by definition.
The lower base angles are congruent.
The upper base angles are congruent.
The lower base angle is supplementary to any upper base angle.