Question

A circle drawn through any point P on the parabola ${{y}^{2}}=4x$ has its centre on the tangent drawn at P. The circle also passes through the point of intersection of tangent and directrix T. Then the circle passes through
(a) (1, 0)
(b) (0, 0)
(c) $\left( \dfrac{1}{2},0 \right)$
(d) (-1, 0)

Answer 1

Hint: First, by using the parametric form, the coordinates of point P can be taken as $\left( {{t}^{2}},2t \right)$. Then, by using the equation of tangent at P is given by $y\times 2t=2\left( x+{{t}^{2}} \right)$. Hen, P and T are the endpoints of the diameter of the circle given and also we can write the equation of the circle as$\left( x+1 \right)\left( x-{{t}^{2}} \right)+\left( y-2t \right)\left( y-t+\dfrac{1}{t} \right)=0$.

Complete step-by-step answer:
In this question, we are supposed to find the point where the circle also passes through the point of intersection of tangent and directrix T.

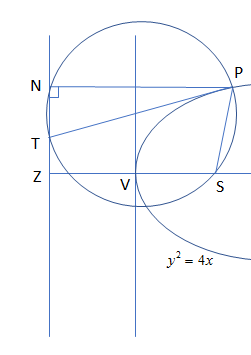
So, we can see from the figure thatcircle through the point P and point T from the figure shown above.
Moreover, its centre will be at some point on the tangent through P and we have the end points of the diameter as point P and has tangent’s intersection with the directrix T.
Now, by using the parametric form, the coordinates of point P can be taken as $\left( {{t}^{2}},2t \right)$.
Now, by using the equation of tangent at P is given by:
$y\times 2t=2\left( x+{{t}^{2}} \right)$
So, the equation of the directrix is x=-1.
Now, the coordinates of point of intersection for the tangent and directrix at T as:
$\left( -1,t-\dfrac{1}{t} \right)$
Since, P and T are the endpoints of the diameter of the circle given and also we can write the equation of the circle as:
$\left( x+1 \right)\left( x-{{t}^{2}} \right)+\left( y-2t \right)\left( y-t+\dfrac{1}{t} \right)=0$
So, from the above equation, (1, 0) satisfies the equation of the circle.
So, the circle passes through the point (1, 0).

So, the correct answer is “Option A”.

Note: Now, to solve these types of questions we need to know some of the basic rules to deal with the tangent to the given curve which is a circle. So, the basic equation of the tangent to the circle is:
$\left( x+1 \right)\left( x-{{t}^{2}} \right)+\left( y-2t \right)\left( y-t+\dfrac{1}{t} \right)=0$ for the directrix as $\left( -1,t-\dfrac{1}{t} \right)$.
Similarly, we can find the equation for any curve.