
A circle C whose radius is 1 unit touches the x – axis at point A. Then centre Q of C lies in the first quadrant. The tangent from the origin O to the circle touches it at T and a point P lies on it such that $\Delta {\text{OAP}}$ is a right – angled triangle at A and its perimeter is 8 units.
The equation of circle C is
(1) ${{\text{(x - 2)}}^2}{\text{ + (y - 1}}{{\text{)}}^2}{\text{ = 1}}$
(2) ${{\text{(x - (}}\sqrt 3 {\text{ - }}\sqrt 2 {\text{))}}^2}{\text{ + (y - 1}}{{\text{)}}^2}{\text{ = 1}}$
(3) ${{\text{(x - }}\sqrt 3 {\text{ )}}^2}{\text{ + (y - 1}}{{\text{)}}^2}{\text{ = 1}}$
(4) none of these
Answer
612.3k+ views
Hint: To solve this question, we will draw a figure according to the question. We will use Pythagoras theorem for the $\Delta {\text{OAP}}$ which is ${\text{O}}{{\text{P}}^2}{\text{ = O}}{{\text{A}}^2}{\text{ + P}}{{\text{A}}^2}$ and also use the distance formula $\sqrt {{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}} $ to find the equation of the circle.
Complete step-by-step answer:
Now, the circle touches the x – axis at point A. Also, the centre of circle Q lies in the first quadrant. The radius of the circle is 1 unit. OT is the tangent from origin O to circle which touches the circle at point T. Point P lies on the tangent OT. So, the figure is
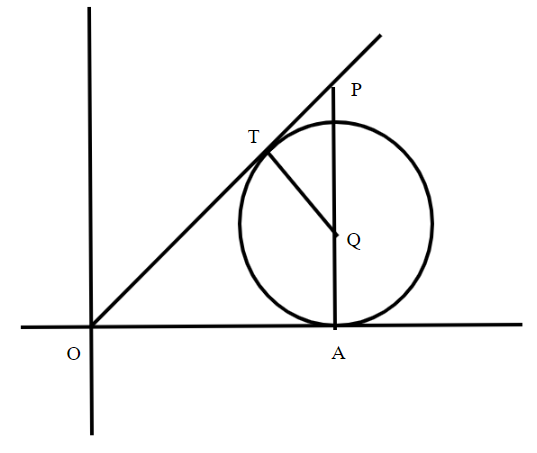
Now, the radius of the circle is 1 unit. So, from the figure, QA = 1 unit and QT = 1 unit. Let the coordinates of centre Q be (h,1). Therefore, the coordinates of point A is (h,0). Let coordinates of point P be (h, k).
Now, the tangent is perpendicular to the radius at the point of contact. So, we get $\angle {\text{OAP = 9}}{{\text{0}}^0}$ and $\angle {\text{QTP = 9}}{{\text{0}}^0}$.
Now, we will apply Pythagoras theorem in $\Delta {\text{OAP}}$,
${\text{O}}{{\text{P}}^2}{\text{ = O}}{{\text{A}}^2}{\text{ + A}}{{\text{P}}^2}$ … (1)
Now, AP = $\sqrt {{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}} $ (By distance formula)
Therefore, AP = $\sqrt {{{({\text{h - h}})}^2}{\text{ + (k - 0}}{)^2}} $ = k units.
OA = $\sqrt {{{({\text{h - 0}})}^2}{\text{ + (0 - 0}}{)^2}} $ = h units.
So, from equation (1), we get
${\text{O}}{{\text{P}}^2}{\text{ = }}{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}$
${\text{OP = }}\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} $
Also, in $\Delta {\text{PQT}}$ applying Pythagoras theorem, we get
${\text{P}}{{\text{Q}}^2}{\text{ = Q}}{{\text{T}}^2}{\text{ + P}}{{\text{T}}^2}$
PQ = $\sqrt {{{({\text{h - h)}}}^2}{\text{ + (k - 1}}{{\text{)}}^2}} $ = (k – 1) units
Therefore, ${\text{P}}{{\text{T}}^2}{\text{ = P}}{{\text{Q}}^2}{\text{ - T}}{{\text{Q}}^2}$
${\text{P}}{{\text{T}}^2}{\text{ = (k - 1}}{{\text{)}}^2}{\text{ - 1}}$
${\text{PT = }}\sqrt {{{{\text{(k - 1)}}}^2}{\text{ - 1}}} $
Also, from an external the length of tangents to circle are equal to each other. So, from point O, OT and OA are tangents of the circle. Therefore, OT = OA = h units.
Now, OP = OT + TP
Putting values, we get
$\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = h + }}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}} $
Squaring both sides, we get
${(\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{)}}^2}{\text{ = (h + }}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}} {)^2}$
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ = }}{{\text{h}}^2}{\text{ + (k - 1}}{{\text{)}}^2}{\text{ - 1 + 2h}}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}} $
On simplification the above term, we get
${\text{k = }}\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}$ … (2)
Now, perimeter of $\Delta {\text{OAP}}$ = 8 units
OA + OP + AP = 8
Putting values in the above expression, we get
${\text{h + k + }}\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = 8}}$
We can write the above expression as,
$\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = 8 - (h + k)}}$
Squaring both sides, we get
${(\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{)}}^2}{\text{ = (8 - (h + k)}}{{\text{)}}^2}$
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ = 64 + }}{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ + 2kh - 16(h + k) }}$
On Simplifying the above expression, we get
${\text{hk - 8(h + k) + 32 = 0}}$
Putting value of k from the equation (2), we get
\[{\text{h}}\left( {\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}} \right){\text{ - 8(h + }}\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}){\text{ }} + {\text{ }}32{\text{ = 0}}\]
\[2{{\text{h}}^3}{\text{ - 8(h(}}{{\text{h}}^2}{\text{ - 1) + 2}}{{\text{h}}^2}){\text{ + 32(}}{{\text{h}}^2}{\text{ - 1) = 0}}\]
On simplification, we get
\[3{{\text{h}}^3}{\text{ - 8}}{{\text{h}}^2}{\text{ - 4h + 16 = 0}}\]
Now, the factors of the above cubic equation are 2,2 and $ - \dfrac{4}{3}$
Now, as the circle lies in the first quadrant, so we take h = 2. So, the centre of circle is Q(h,1) i.e. Q(2,1). Also, the radius of the circle is 1 unit.
Now, the equation of a circle is written as
${{\text{(x - }}{{\text{x}}_1})^2}{\text{ + (y - }}{{\text{y}}_1}{)^2}{\text{ = }}{{\text{r}}^2}$, where (${{\text{x}}_1},{{\text{y}}_1}$) are the coordinates of the centre of the circle and r is the radius of the circle.
On putting values, we get
${({\text{x - 2)}}^2}{\text{ + (y - 1}}{{\text{)}}^2}{\text{ = 1}}$
So, the equation of circle is ${({\text{x - 2)}}^2}{\text{ + (y - 1}}{{\text{)}}^2}{\text{ = 1}}$. So, option (1) is correct.
Note: When we come up with such types of questions, we have to first draw a figure according to the question. Such questions can’t be solved without a figure. So, a figure is necessary to solve the given problem. Also, we have used some properties of tangent to circle. All the properties should be used carefully to solve the question. Pythagoras theorem is also used to solve this question.
Complete step-by-step answer:
Now, the circle touches the x – axis at point A. Also, the centre of circle Q lies in the first quadrant. The radius of the circle is 1 unit. OT is the tangent from origin O to circle which touches the circle at point T. Point P lies on the tangent OT. So, the figure is
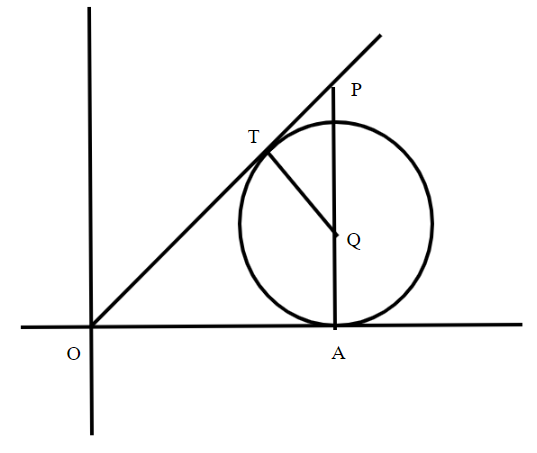
Now, the radius of the circle is 1 unit. So, from the figure, QA = 1 unit and QT = 1 unit. Let the coordinates of centre Q be (h,1). Therefore, the coordinates of point A is (h,0). Let coordinates of point P be (h, k).
Now, the tangent is perpendicular to the radius at the point of contact. So, we get $\angle {\text{OAP = 9}}{{\text{0}}^0}$ and $\angle {\text{QTP = 9}}{{\text{0}}^0}$.
Now, we will apply Pythagoras theorem in $\Delta {\text{OAP}}$,
${\text{O}}{{\text{P}}^2}{\text{ = O}}{{\text{A}}^2}{\text{ + A}}{{\text{P}}^2}$ … (1)
Now, AP = $\sqrt {{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}} $ (By distance formula)
Therefore, AP = $\sqrt {{{({\text{h - h}})}^2}{\text{ + (k - 0}}{)^2}} $ = k units.
OA = $\sqrt {{{({\text{h - 0}})}^2}{\text{ + (0 - 0}}{)^2}} $ = h units.
So, from equation (1), we get
${\text{O}}{{\text{P}}^2}{\text{ = }}{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}$
${\text{OP = }}\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} $
Also, in $\Delta {\text{PQT}}$ applying Pythagoras theorem, we get
${\text{P}}{{\text{Q}}^2}{\text{ = Q}}{{\text{T}}^2}{\text{ + P}}{{\text{T}}^2}$
PQ = $\sqrt {{{({\text{h - h)}}}^2}{\text{ + (k - 1}}{{\text{)}}^2}} $ = (k – 1) units
Therefore, ${\text{P}}{{\text{T}}^2}{\text{ = P}}{{\text{Q}}^2}{\text{ - T}}{{\text{Q}}^2}$
${\text{P}}{{\text{T}}^2}{\text{ = (k - 1}}{{\text{)}}^2}{\text{ - 1}}$
${\text{PT = }}\sqrt {{{{\text{(k - 1)}}}^2}{\text{ - 1}}} $
Also, from an external the length of tangents to circle are equal to each other. So, from point O, OT and OA are tangents of the circle. Therefore, OT = OA = h units.
Now, OP = OT + TP
Putting values, we get
$\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = h + }}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}} $
Squaring both sides, we get
${(\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{)}}^2}{\text{ = (h + }}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}} {)^2}$
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ = }}{{\text{h}}^2}{\text{ + (k - 1}}{{\text{)}}^2}{\text{ - 1 + 2h}}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}} $
On simplification the above term, we get
${\text{k = }}\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}$ … (2)
Now, perimeter of $\Delta {\text{OAP}}$ = 8 units
OA + OP + AP = 8
Putting values in the above expression, we get
${\text{h + k + }}\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = 8}}$
We can write the above expression as,
$\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = 8 - (h + k)}}$
Squaring both sides, we get
${(\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{)}}^2}{\text{ = (8 - (h + k)}}{{\text{)}}^2}$
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ = 64 + }}{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ + 2kh - 16(h + k) }}$
On Simplifying the above expression, we get
${\text{hk - 8(h + k) + 32 = 0}}$
Putting value of k from the equation (2), we get
\[{\text{h}}\left( {\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}} \right){\text{ - 8(h + }}\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}){\text{ }} + {\text{ }}32{\text{ = 0}}\]
\[2{{\text{h}}^3}{\text{ - 8(h(}}{{\text{h}}^2}{\text{ - 1) + 2}}{{\text{h}}^2}){\text{ + 32(}}{{\text{h}}^2}{\text{ - 1) = 0}}\]
On simplification, we get
\[3{{\text{h}}^3}{\text{ - 8}}{{\text{h}}^2}{\text{ - 4h + 16 = 0}}\]
Now, the factors of the above cubic equation are 2,2 and $ - \dfrac{4}{3}$
Now, as the circle lies in the first quadrant, so we take h = 2. So, the centre of circle is Q(h,1) i.e. Q(2,1). Also, the radius of the circle is 1 unit.
Now, the equation of a circle is written as
${{\text{(x - }}{{\text{x}}_1})^2}{\text{ + (y - }}{{\text{y}}_1}{)^2}{\text{ = }}{{\text{r}}^2}$, where (${{\text{x}}_1},{{\text{y}}_1}$) are the coordinates of the centre of the circle and r is the radius of the circle.
On putting values, we get
${({\text{x - 2)}}^2}{\text{ + (y - 1}}{{\text{)}}^2}{\text{ = 1}}$
So, the equation of circle is ${({\text{x - 2)}}^2}{\text{ + (y - 1}}{{\text{)}}^2}{\text{ = 1}}$. So, option (1) is correct.
Note: When we come up with such types of questions, we have to first draw a figure according to the question. Such questions can’t be solved without a figure. So, a figure is necessary to solve the given problem. Also, we have used some properties of tangent to circle. All the properties should be used carefully to solve the question. Pythagoras theorem is also used to solve this question.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




