Question

A church tower stands on the bank of a river, which is 150 feet wide, and on the top of the tower is a spire 30 feet high. To an observer on the opposite bank of the river, the Spiro subtends the same angle that a pole six feet high subtends when placed upright on the ground at the foot of the tower. Prove that the height of the tower is nearly 285 feet

Answer 1

Hint: In this question distance of the church from the river bank is given and height of the spite is given so by applying the angle of elevation we will find the height of the church by comparing the two equations observed, one the height of church and other the total height of church and the spire.

Complete step-by-step answer:
Distance between church tower and the river bank \[ = 150ft\]
Height of the spire\[ = 30ft\]
Now let the angle subtended by the Spiro to an observer on the river bank of river be \[\alpha \]
It is said that the angle subtended by the Spiro is same as the angle subtended by the pole which is at the ground as shown in the diagram below

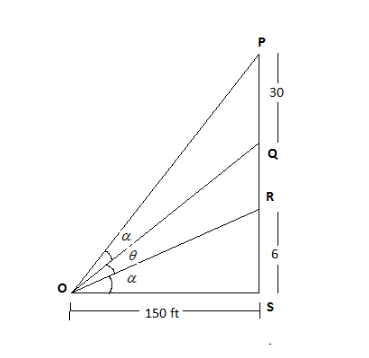
From the figure
\[\angle POQ = \angle ROS = \alpha \] {Same angle subtended by observer}
Now consider \[\Delta ROS\]
Here
\[\tan \alpha = \dfrac{{RS}}{{OS}} = \dfrac{6}{{150}} = \dfrac{1}{{25}} - - (i)\]
Now let the height \[QS = h - - (ii)\]
Also \[\angle QOR = \theta \]
Hence we can say
\[\angle POS = 2\alpha + \theta - - (iii)\]
Now in \[\Delta QOS\]
\[\tan \left( {QOS} \right) = \dfrac{h}{{150}} - - (iv)\]
In \[\Delta POS\]
\[\tan \left( {POS} \right) = \dfrac{{h + 30}}{{150}} - - (v)\]
Now we can write
\[\tan \left( {2\alpha + \theta } \right) = \tan \left( {\alpha + \alpha + \theta } \right)\]
Hence by substituting the values from the equation (v) we can write
\[
\Rightarrow \dfrac{{h + 30}}{{150}} = \dfrac{{\dfrac{h}{{150}} + \dfrac{6}{{150}}}}{{1 - \dfrac{h}{{150}} \cdot \dfrac{6}{{150}}}} \\
  \dfrac{{h + 30}}{{150}} = \dfrac{{h + 6}}{{150 - 6h}} \;
 \]
Now by cross multiplying, we get
\[
\Rightarrow 150h - 6{h^2} + 4500 - 180h = 150h + 900 \\
\Rightarrow 6{h^2} + 180h - 5400 = 0 \\
\Rightarrow {h^2} + 30h - 900 = 0 \;
 \]
By solving the obtained quadratic equation we get the height
\[
\Rightarrow h = 15\left( {\sqrt {401} - 1} \right) \\
   = 285ft \;
 \]
Hence, the height of the tower is nearly 285 feet

Note: Students should not be confused with the angle of elevation and the angle of depression. These are two different things. The angle of elevation is the rising angle generally, from the foot while the angle of depression is measured for the top of the tower.