Question

A chord AB is at a distance of $6cm$ from the centre of a circle whose radius is $6 cm$ less than that of the chord AB. Find the length of the chord AB.
(A) $8cm$
(B) $32cm$
(C) $24cm$
(D) $16cm$

Answer 1

Hint: Draw a diagram with all the information given in the question. Now draw a perpendicular from the centre of the circle to the chord and name it OM. Assume the length of chord AB as some variable. Now you can consider a right-angles triangle OMB, and apply Pythagoras theorem to obtain a relation. Now solve the equation to find the value of the assumed variable.

Complete step-by-step answer:
               

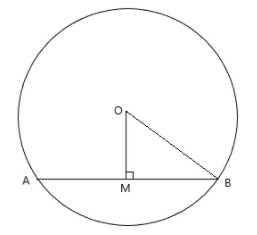
According to the given information, let's draw a diagram to visualise the problem better. So, here we have a chord AB and it is at a distance of $6cm$ from the centre O of a circle. Therefore, we can draw a perpendicular bisector OM from centre to the chord, and it will be of length $6cm$. It is also given that the radius of the circle is $6cm$ less than the length of chord AB.
Therefore, we can assume the length of the chord AB as $n{\text{ cm}}$ and we get the radius of the circle as $\left( {n - 6} \right){\text{ cm}}$.
$ \Rightarrow OM = 6{\text{ cm}},OB = \left( {n - 6} \right){\text{ cm}},AB = n{\text{ cm and }}MB = \dfrac{n}{2}cm$
As we know the Pythagoras’ theorem, which states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of the other two sides of the right-angled triangle. Or, the sum of the squares of the two legs of a right triangle is equal to the square of its hypotenuse.
$ \Rightarrow {\text{In }}\Delta OMB,{\text{ }}O{B^2} = M{B^2} + O{M^2}$
Let’s substitute the know values in the above relation, this will give us:
$ \Rightarrow O{B^2} = M{B^2} + O{M^2}$
$\Rightarrow {\left( {n - 6} \right)^2} = {\left( {\dfrac{n}{2}} \right)^2} + {6^2}$
Now we can solve this quadratic equation using ${\left( {a - b} \right)^2} = {a^2} + 2ab + {b^2}$ for the value of $n$
$ \Rightarrow {n^2} - 12n + 36 = \dfrac{{{n^2}}}{4} + 36$
$\Rightarrow 4{n^2} - 48n = {n^2}$
$\Rightarrow 3{n^2} - 48n = 0$
$\Rightarrow n\left( {3n - 48} \right) = 0$
So, we get two root $n = 0{\text{ or }}n = \dfrac{{48}}{3} = 16$
Therefore, we can say that length of the chord AB is $16 cm$

So, the correct answer is “Option D”.

Note: Try to draw a diagram while understanding the question for better visualisation of the problem. Note that we used a property of the circle according to which if you draw a line perpendicular to the chord, it will divide the chord into two equal parts. This allowed us to conclude that $MB = \dfrac{1}{2} \times AB$. Also notice that in the quadratic equation we selected the root that is a positive whole number, not the value $n = 0$ because here $n$ is the length of chord, which cannot be zero.