Question

A child walks 6 m towards the west and then 20 in towards the south. He then turns east and walks another 12 m. Then he walks 12 m towards the north. How far is he from his initial position?

Answer 1

Hint: We first draw the locus of the path the child covered. We use the concept of rectangle and Pythagoras’ theorem to find the required distance in the form of hypotenuse. We take opposite sides of the rectangle as equal to find the length of the extended lines.

Complete step by step answer:
A child starts from A, walks 6 m towards the west to reach B, then 20 in towards south to reach C. He then turns east and walks another 12 m and reaches D. Then he walks 12 m towards the north and reach point E. So, $AB=6,BC=20,CD=12,DE=12$.

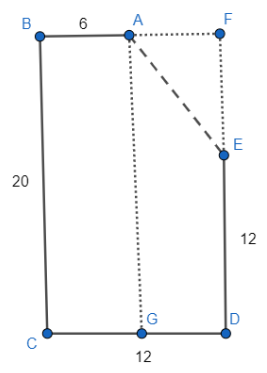
We need to find the distance from his initial position being equal to AE. The angle between the direction changes of the child is at right-angle. In the picture the angles which are at right-angle are $\angle ABC=\angle BCD=\angle CDE=\angle ABC={{90}^{\circ }}$.

Now we draw the lines AF and EF which are the extensions of BA and DE respectively and they meet at point F at the right-angle also. So, in FBCD we have four angles equal to ${{90}^{\circ }}$. Therefore, depending on the opposite sides, FBCD becomes a rectangle. We get $BC=FD=20,BF=CD=12$.

Subtracting we get $EF=FD-DE=20-12=8$ and $AF=BF-AB=12-6=6$.
Now using the Pythagoras’ theorem of $bas{{e}^{2}}+heigh{{t}^{2}}=hypotenus{{e}^{2}}$ for right-angle triangle $\Delta AEF$, we get $A{{F}^{2}}+F{{E}^{2}}=A{{E}^{2}}={{6}^{2}}+{{8}^{2}}=100$
We get $AE=\sqrt{100}=10$.

Therefore, the child is 10 m far from his initial position.

Note: The concept of Pythagorean identity is similar for both angles and sides. The representation of the triangle has to be for the right-angle triangle. We can also represent it as the ratio of the angles. We get ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$. We also cannot take the cumulative distance of AF and FE as summation to find distance as distance means the shortest way to reach from one point to another in a straight line.