Question

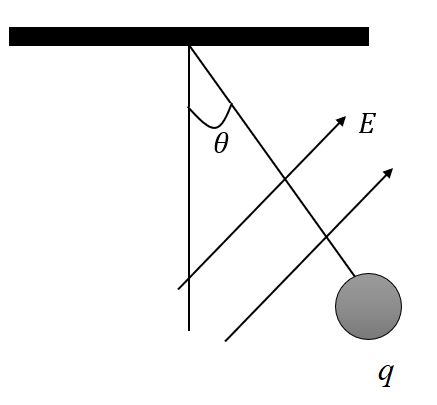
A charged cork ball of mass m is suspended on a light string in the presence of a uniform electric field as shown in the figure. When \[E = \left( {A\hat i + B\hat j} \right)\,N{C^{ - 1}}\], where A and B are positive numbers. The ball is in equilibrium at an angle \[\theta \]. Find the charge on the ball?

A. \[q = \dfrac{{mg}}{{A + B\tan \theta }}\]
B. \[q = \dfrac{{mg\tan \theta }}{{A + B}}\]
C. \[q = \dfrac{{mg\tan \theta }}{{A + B\tan \theta }}\]
D. \[q = \dfrac{{Amg}}{{A + B}}\]

Answer 1

Hint: Balance the forces acting on the ball in horizontal direction and vertical direction separately.\[F = qE\] Here, q is the charge on the ball and E is the electric field.is used to find out the answer.

Complete step by step answer:
According to Coulomb’s law, the expression for the force due electric field is,
\[F = qE\]

Here, q is the charge on the ball and E is the electric field.

The other forces acting on the ball are the weight of the ball and the tension in the string as shown in the figure below,

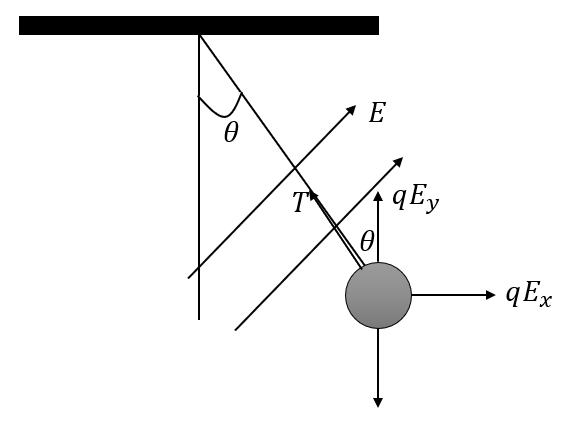
The net force acting on the ball in the horizontal direction is,
\[q{E_x} - T\sin \theta = 0\]
\[ \Rightarrow T\sin \theta = q{E_x}\] …… (1)

The net force acting on the ball in the vertical direction is,
\[T\cos \theta + q{E_y} - mg = 0\]
\[ \Rightarrow T\cos \theta + q{E_y} = mg\]
\[ \Rightarrow T\cos \theta = mg - q{E_y}\] …… (2)
Divide equation (1) by equation (2).
\[\dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{q{E_x}}}{{mg - q{E_y}}}\]
\[\tan \theta = \dfrac{{q{E_x}}}{{mg - q{E_y}}}\] …… (3)

The given equation of electric field is,
\[E = \left( {A\hat i + B\hat j} \right)\,N{C^{ - 1}}\]

Here, A is the horizontal component of the electric field and B is the vertical component of the electric field.
Therefore, substitute A for \[{E_x}\] and B for \[{E_y}\] in equation (3).
\[\tan \theta = \dfrac{{qA}}{{mg - qB}}\]

Rearrange the above equation as follows,
\[\left( {\tan \theta } \right)\left( {mg - qB} \right) = qA\]

\[ \Rightarrow mg\tan \theta - qB\tan \theta = qA\]
\[ \Rightarrow mg\tan \theta = qA + qB\tan \theta \]
\[ \Rightarrow mg\tan \theta = q\left( {A + B\tan \theta } \right)\]
\[\therefore q = \dfrac{{mg\tan \theta }}{{A + B\tan \theta }}\]

So, the correct answer is Option C .

Note:
The ball does not move in any direction. Therefore, the acceleration of the ball is zero. Thus, the net force in the horizontal direction and along the vertical direction is zero.