Question

A charge of $8mC$ is located at the origin. Calculate the work done in moving a small charge of $-2\times {{10}^{-9}}C$ from a point $P\left( 0,0,3cm \right)$, $Q\left( 0,4cm,0 \right)$ via a point $R\left( 0,6cm,9cm \right)$.

Answer 1

Hint: The initial distance between the charges should be found from both the points. Then calculate the work done taking the small charge from P to Q. this depends on the initial and final position only. That is dependent on the path followed. These all may help you to solve this question.

Complete step by step answer:
from the question, we can understand that a bigger charge is located at the origin which is having a magnitude given by,
$q=8mC=8\times {{10}^{-3}}C$
And also a smaller charge is having a magnitude given as,
${{q}_{0}}=-2\times {{10}^{-9}}C$
This smaller charge is being taken from the point$P\left( 0,0,3cm \right),Q\left( 0,4cm,0 \right)\text{ via a point }R\left( 0,6cm,9cm \right)$
This has been shown in the figure.

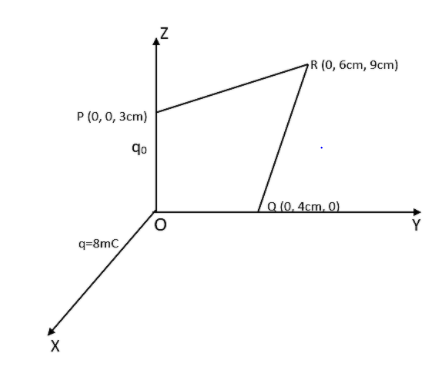
Let us assume that the initial distance between larger charge $q$ and smaller charge ${{q}_{0}}$ are given as ${{r}_{P}}$. The value of this separation is determined as,
\[{{r}_{P}}=3cm=0.03m\]
And the final separation between the larger charge and the smaller charge is given by the equation,
\[{{r}_{Q}}=4cm=0.04m\]
Therefore the work done in taking the charge from the point P to Q can be found out. It is not dependent on the path followed. It depends only on the initial and final positions of the charges. That is the distance between \[{{r}_{Q}}\text{ and }{{r}_{P}}\].
Hence we can write that the work done will be,
\[W=\dfrac{1}{4\pi {{\varepsilon }_{0}}}q{{q}_{0}}\left[ \dfrac{1}{{{r}_{Q}}}-\dfrac{1}{{{r}_{P}}} \right]\]
Where \[{{\varepsilon }_{0}}\] be the permittivity of the medium.
So let us substitute the given values in it to get the answer.
\[W=9\times {{10}^{9}}\times 8\times {{10}^{-3}}\times -2\times {{10}^{-9}}\left[ \dfrac{1}{0.04}-\dfrac{1}{0.03} \right]\]
That is firstly we can do the brackets of the equation,
\[W=9\times {{10}^{9}}\times 8\times {{10}^{-3}}\times -2\times {{10}^{-9}}\times \left[ \dfrac{-0.01}{1.2\times {{10}^{-3}}} \right]\]
Now we can do the multiplications in the equation,
\[W=\dfrac{1.44\times {{10}^{-3}}}{1.2\times {{10}^{-3}}}\]
Simplifying this equation will give,
\[W=1200\times {{10}^{-3}}J=1.2J\]
Therefore the correct answer for the question has been obtained. The work done to take the charge from P to Q has been calculated.

Note:
The permittivity of free space is found to be a physical constant frequently used in electromagnetism. It indicates the ability of a vacuum to allow electric fields. It is used to define the energy stored within an electric field and capacitance.