Question

A charge of $5 \times {10^{10}}C$ is given to a metal cylinder of length $10cm$, placed in the air. The electric intensity due to the cylinder at a distance of $0.2m$form its axis is: -
A. $150V/m$
B. $250V/m$
C. $350V/m$
D. $450V/m$

Answer 1

Hint: Use the concept of Gaussian surface and gausses’ law for electric field intensity at a point due long current carrying conductor of cylindrical shape OR wine.

Formulae used:
$E = \dfrac{\lambda }{{2\pi r{ \in _0}}}$
$\lambda $ is linear change density
$r$ is the radius of a Gaussian cylinder.
 ${ \in _0}$ is permittivity in the free space

Complete step by step answer:
Observe the diagram

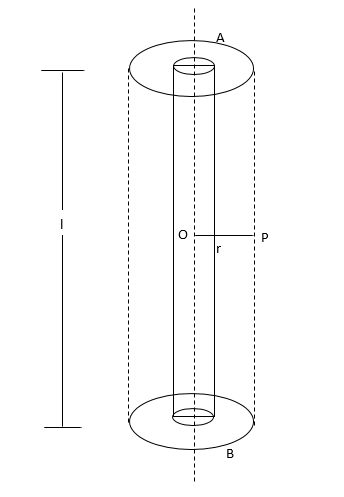
Let \[AB\] be a cylinder of length,
$l = 10cm = 0.1m$
Let $O$ be some point on the axis of the cylinder.
Let $P$ be some point, close to cylinder such that,
$OP = r = 0.2m$
$Q = 5 \times {10^{ - 10}}C$ is the given change on the cylinder.
Now, assume a cylinder, concurrent to the given cylinder, such that the radius of the Gaussian cylinder is $r = 0.2m$.
Then the point P lies on the edge of the Gaussian surface.
Now, according to Gauss’s law. Electric field intensity due to a large cylindrical current carrying conductor is at point $P$ given by,
$E = \dfrac{\lambda }{{2\pi r{ \in _0}}}$ . . . (1)
Where,
$\lambda $ is linear change density
$r$ is the radius of a Gaussian cylinder.
${ \in _0}$ is permittivity in the free space
${ \in _0} = 8.85 \times {10^{ - 12}}{c^2}N{m^{ - 2}}$
To solve equation (1), we need, value of$\lambda $
For that we know,
Linear change density is the ratio of total change on the conductor and the length of the conductor
i.e. $\lambda = \dfrac{Q}{l}$
By substituting the given values, we get
$\lambda = \dfrac{{5 \times {{10}^{ - 10}}}}{{0.1}}$
$ \Rightarrow \lambda = 5 \times {10^{ - 9}}C/m$ $\left( {\because \dfrac{{{a^m}}}{{{a^n}}} = {a^{m - n}}} \right)$
Substituting this values in equation (1), we get
$E = \dfrac{\lambda }{{2\pi r{ \in _0}}}$
$ = \dfrac{{5 \times {{10}^{ - 9}}}}{{2 \times 3.14 \times 0.2 \times 885 \times {{10}^{ - 12}}}}$ $\left( {\because \pi = 3.14 = \dfrac{{22}}{7}} \right)$
$ = \dfrac{{5 \times {{10}^{ - 9}}}}{{2 \times 314 \times {{10}^{ - 2}} \times 2 \times {{10}^{ - 1}} \times 885 \times {{10}^{ - 2}} \times {{10}^{ - 12}}}}$
$ = \dfrac{{5 \times {{11}^{ - 9}}}}{{4 \times 314 \times 885 \times {{10}^{ - 17}}}}$ $\left( {\because {a^m}{a^n} = {a^{m - n}}} \right)$
$ = \dfrac{{1 \times {{10}^{ - 9 + 17}}}}{{1256 \times 177}}$
$ = \dfrac{1}{{1256 \times 177}} \times {10^8}$
$ \Rightarrow E = 449.8V/m$
$ \Rightarrow E \approx 450V/m$
Therefore, the electric field intensity at point $P$ is $450V/m$.
Therefore, from the above explanation, the correct answer is, option (D) $450V/m$

Note:
Calculation can be difficult in such questions. You should use a log table for complex calculation.
Since this question is objective, single current type, we can simplify the calculation by approximating the calculation as well.
For example, one of the steps in above solution is
$E = \dfrac{{5 \times {{10}^{ - 11}}}}{{2 \times 3.14 \times 0.2 \times {{10}^{ - 1}} \times 8.85 \times {{10}^{ - 12}}}}$
Write, $3.14 \approx 3$, and$8.85 \approx 9$
We get,
$E = \dfrac{{5 \times {{10}^{ - 11}} \times {{10}^{12}}}}{{2 \times 3 \times 0.2 \times 9}}$
$ = \dfrac{{5 \times 10}}{{54 \times 0.2}}$.