Question

A charge of $4 \times {10^{ - 9}}C,$ is distributed uniformly over the circumference of a conducting ring, of radius $0.3m.$ Calculate the field intensity at a point on the axis of the ring, at $0.4m$ from its center and also at the center.

Answer 1

Hint:Here we are going to use the concept of electric field intensity at a point on the axis of the ring and after some assumptions and calculations we arrive at the desired result.

Formula used:
${E_x} = \dfrac{{qx}}{{4\pi {\varepsilon _0}{{({R^2} + {x^2})}^{3/2}}}}$

Complete step by step answer:

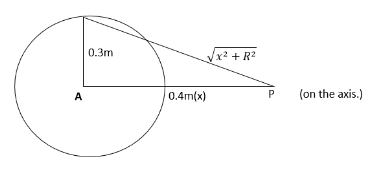
The given information in the question is:
Charge on the ring, $q = 4 \times {10^{ - 9}}C$
Radius of the ring, $R = 0.3m$
Distance of a given point from the ring is $x = 0.4m$
We know that the electric field intensity at a point P, lying on the axis of the ring, at some distance $x$ from the center is given by
${E_x} = \dfrac{{qx}}{{4\pi {\varepsilon _0}{{({R^2} + {x^2})}^{3/2}}}}$ . . . (1)
Where,
${E_x}$ is electric field intensity along x-axis
$q$ is the charge on the ring
$x$ is the distance of a given point from the center of the ring.
\[R\] is the radius of the ring
Hence, Electric field intensity from its center at a distance $x = 0.4m.$
$ \Rightarrow {E_x} = \dfrac{{qx}}{{4\pi {\varepsilon _0}{{({R^2} + {x^2})}^{3/2}}}}$
Now by substituting the values given in the question, we have
${E_x} = \dfrac{{9 \times {{10}^9} \times 4 \times {{10}^{ - 9}} \times 0.4}}{{{{({{0.4}^2} + {{0.3}^2})}^{3/2}}}}$
$ = \dfrac{{1404 \times 2}}{{{{(0.5)}^2}}}$
$ = \dfrac{{28.8}}{{0.25}}$
$\therefore {E_x} = 115.2N/C$
Therefore, the value of electric field intensity at a distance $x = 0.4m$from its center is ${E_x} = 115.2N/C$
Now, if we assume the given point is at the center of the ring then the distance between the point and the center of the ring will be zero. i.e. $x = 0.$
Put this value of $x$in equation (1)
${E_x} = \dfrac{{qx}}{{4\pi {\varepsilon _0}{{({R^2} + {x^2})}^{3/2}}}}$
$ \Rightarrow {E_x} = \dfrac{{q \times 0}}{{4\pi {\varepsilon _0}{{({R^2} + 0)}^{3/2}}}}$
$ \Rightarrow {E_x} = 0$ (Since, any value multiplied by zero is equal to zero)

Note:We can use the concept of this question to remember the fact that the electric field intensity at the center of any hollow charged conductor is zero so it is a useful point to be remembered as it helps us in solving various kinds of numerical problems.