Question

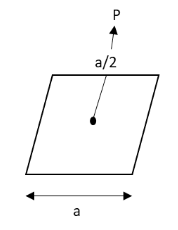
A charge is placed at a distance \[a/2\] above the centre of a square surface of edge \[a\] as shown in the figure. The electric flux through the square surface is:

A. \[\dfrac{Q}{{3{\varepsilon _0}}}\]
B. \[\dfrac{Q}{{6{\varepsilon _0}}}\]
C. \[\dfrac{Q}{{2{\varepsilon _0}}}\]
D. \[\dfrac{Q}{{{\varepsilon _0}}}\]

Answer 1

Hint:Use the formula for the electric flux through a closed surface. This formula gives the relation between the electric flux through the closed surface, charge and permittivity of free space. First draw an imaginary cube around the charge with the charge placed at the centre of the cube. Then determine the electric flux through only one face of the cube which is the required answer.

Formula used:
The electric flux \[\phi \] passing through a closed area is given by
\[\phi = \dfrac{Q}{{{\varepsilon _0}}}\] …… (1)
Here, \[Q\] is the charge enclosed in the area and \[{\varepsilon _0}\] is the permittivity of free space.

Complete step by step answer:
We have given that a charge is placed at a distance \[a/2\] above the centre of a square surface of edge \[a\] as shown in the figure.We have asked to determine the electric flux through the square surface.We know that the electric flux through any closed surface is the number of electric field lines passing through that surface.

We have given that the charge is placed above the square surface. To determine the electric flux through the given surface, we need to construct an imaginary cube around the charge with the charge placed at the centre of the cube.Let us draw the diagram of the imaginary cube around the charge.

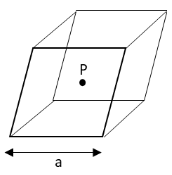
We can see that the electric flux due to this charge Q passes through all the six sides of the imaginary cube.But we have asked for the electric flux through only one given square shaped surface of the cube.Thus, the net electric flux through one square shaped surface is one sixth of the total electric flux through the whole imaginary cube.
According to equation (1), the electric flux through one surface is
\[\phi = \dfrac{1}{6} \times \dfrac{Q}{{{\varepsilon _0}}}\]
\[ \therefore \phi = \dfrac{Q}{{6{\varepsilon _0}}}\]
Therefore, the electric flux through the square surface is \[\dfrac{Q}{{6{\varepsilon _0}}}\].

Hence, the correct option is B.

Note: The students should keep in mind that we have asked to determine the electric flux through only one given square shaped surface. The students may get confused and determine the electric flux through the whole imaginary cube around the charge. But this is not the required answer. One should determine one sixth of the total flux through the cube.