Question

A certain transition to the $H$ spectrum from an excited state to ground state in one or more steps gives rise to a total of $10$ lines. How many of these belong to the UV spectrum?
A. $3$
B. $4$
C. $5$
D. $6$

Answer 1

Hint:As we are given that the lower energy level is the ground state, we can use the formula for finding the number of spectral lines to determine the excited state level. The UV radiations in the spectrum only correspond to the Lyman series, that is, when transitions occur to the first energy level. Hence, if we get the excited state level, we can draw the energy level diagram to count the number of lines that fall onto the first energy level.
Formulas used: Number of lines observed when transition occurs to the ground state:
Number of spectral lines = $\dfrac{{n(n - 1)}}{2}$
Where $n$ is the higher energy level

Complete step by step answer:
We are given that the transition occurs to the ground state. That is, the lower energy level is the first shell. Our next job is to find a higher energy level. For this, we make use of the formula which gives us the number of lines observed when transition occurs to the ground state:
Number of spectral lines = $\dfrac{{n(n - 1)}}{2}$
Where $n$ is the higher energy level
We are given that the total number of lines observed is ten. Substituting this, we get:
$10 = \dfrac{{n(n - 1)}}{2} \Rightarrow 20 = {n^2} - n$
We have to solve this quadratic to get the value of $n$.
${n^2} - n - 20 = 0 \Rightarrow {n^2} - 5n + 4n - 20 = 0$
Selecting the common term and factoring, we get:
$n(n - 5) + 4(n - 5) = 0$
Hence, we get:
$(n - 5)(n + 4) = 0 \Rightarrow n = 5,n = - 4$
We choose the value of $n = 5$ as $n$ cannot be a negative number.
Now, we know that in the spectrum of Hydrogen, UV lines occur only in the Lyman series, that is, when the transition occurs from higher states to the ground state (first energy level). Here, as the highest energy level as we found out is $n = 5$, the Lyman series can have transitions from $n = 5$ to $n = 1$, $n = 4$ to $n = 1$, $n = 3$ to $n = 1$ and $n = 2$ to $n = 1$. Thus, there are four transitions which can take place in the Lyman series, all which corresponds to UV light. The energy level diagram of the UV radiations would look like this:

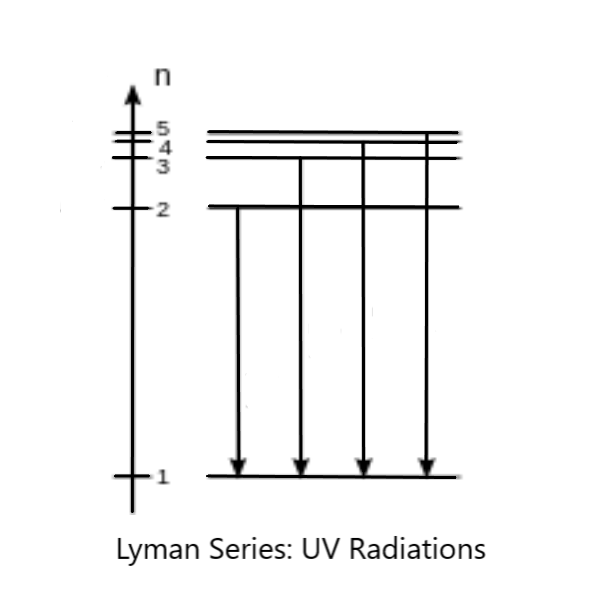
Thus, the correct option to be marked is option B.

Note:
The transitions from all levels are due to the result of de-excitation from level five. For example, in the transition from $n = 3$ to $n = 1$, the electron first gets de-excited from $n = 5$ to $n = 3$ (this transition would lie in the Paschen series, and hence, would be emitted as infrared radiation) and then from there to the ground state. Note that the rest of the six lines (emissions other than UV) out of the ten are observed due to the de-excitation to the second, third and fourth levels.