Question

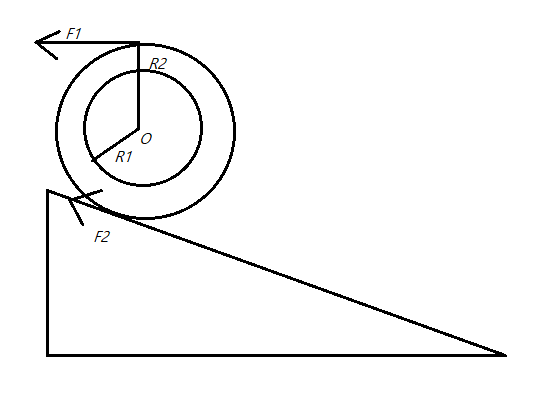
A certain bicycle can go up a gentle inclination with a constant speed when the frictional force of ground pushing the rear wheel in $F_{2}=4N$. If $R_{1}=5m$ and $R_{2}=30m$, then what will be the force $F_{1}$ with which the chain must pull on the sprocket wheel?

\[\begin{align}
  & A.4N \\
 & B.24N \\
 & C.140N \\
 & D.\dfrac{35}{4}N \\
\end{align}\]

Answer 1

Hint: To find $F_{1}$, we need to understand that due, to rolling, angular acceleration $\omega=constant$, then the torque $\tau=0$, due to which we get, $F_{1}R_{1}-F_{2}R_{2}=0$, as the forces are acting in the opposite directions. Now substituting the given values, we get, $F_{1}$

Formula used:
$\tau=F\times R$

Complete answer:
Given that the bicycle goes up the inclination at a constant velocity say $v$, then the acceleration$a=0$.
Due to rolling, we have, $v=\omega R$, where, $\omega$ is the angular velocity, and $R$ is the radius of the body.
Since \[v,R\] is constant, and then $\omega$ is also constant.
If $\omega=constant$, then, torque i.e. \[\tau =0\].
Since, torque acts at the centre, $\tau=F\times R$
 Now, the forces $F_{1},F_{2}$ are opposite to each other.
Then we get,
$F_{1}R_{1}-F_{2}R_{2}=0$
Or$F_{1}R_{1}=F_{2}R_{2}$
Then, $F_{1}=\dfrac{F_{2}R_{2}}{R_{1}}$
Given that $F_{2}=4N$, $R_{1}=5m$, and $R_{2}=30m$. Substituting we get, $F_{1}=\dfrac{4\times 30}{5}=24N$

Hence the answer is \[B.24N\]

Additional Information:
Angular velocity $\omega$ is the measure of how fast an object moves with respect to time. There are two types of angular velocity: namely orbital angular velocity, this denotes the time rate of change of its angular position relative to the origin and spin angular velocity is the measure of how fast the body rotates with respect to its centre of rotation. Clearly, spin angular velocity is independent of the origin.
Similarly, torque is defined as the product of the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation.

Note:
We don’t use the angle of inclination here, at all. Instead, we use the rotational properties, like angular velocity, and torque to solve the problem. The $\omega$ is a constant, as \[v,R\] is constant. Then the torque \[\tau =0\]. Since the forces $F_{1},F_{2}$ are opposite to each other, $F_{1}R_{1}-F_{2}R_{2}=0$