Question

A centrifuge accelerates uniformly from rest to 15,000 rpm in 220 s. Through how many revolutions did it turn in this time?

Answer 1

Hint: To calculate the number of revolutions made by accelerating the centrifuge from rest, we divide the total displacement (computed from its acceleration using the equations of motion) in the given amount of time by $2\pi $ radians (1 revolution $=2\pi $ radians).

Complete answer:
A centrifuge is a machine which rotates in high speed and uses centrifugal force to separate fluids of different densities or to separate suspended solid particles in liquids. It has a container which holds the substance and rotates with high speed with the help of the motor as shown in the figure below.

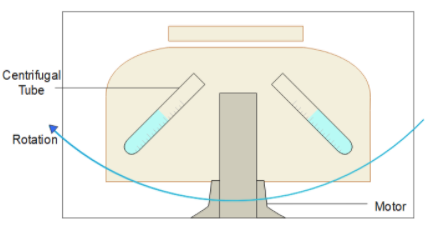
Centrifuge uses the principle of centrifugal force, which is a force that comes into play due to an object’s inertia, that is moving in a circular path and its direction is inwards towards the centre of the circular path.

According to the question, the centrifuge accelerates uniformly from rest to 15,000 rpm.

Hence, the initial angular velocity is zero (${{\omega }_{i}}=0$). The final angular velocity is,
${{\omega }_{f}}=15000\times 2\pi \times \dfrac{1}{60}=500\pi $ radians/ s ….(i)

The angular acceleration is given by,
$a=\dfrac{{{\omega }_{f}}-{{\omega }_{i}}}{t}=\dfrac{500\pi -0}{220}=7.1364$ radians /${{s}^{2}}$ ….(ii) (since, $t=220s$)

Now, we calculate the total angular displacement using the rotational kinematic equation of motion, we get,
$\theta ={{\omega }_{i}}+\dfrac{1}{2}a{{t}^{2}}$
$\Rightarrow \theta =0+\dfrac{1}{2}\times 7.1364\times {{(220)}^{2}}=172700=1.727\times {{10}^{5}}$radians (since, ${{\omega }_{i}}=0$)

The number of revolutions is given by dividing the total displacement by $2\pi $ radians, since we know 1 revolution $=2\pi $ radians, we get,
$\dfrac{1.727\times {{10}^{5}}}{2\pi }=27500=2.75\times {{10}^{4}}$ revolutions

Thus, when a centrifuge accelerates uniformly from rest to 15,000 rpm in 220 seconds it turns $2.75\times {{10}^{4}}$ revolutions in this amount of time.

Note:
It is important to remember the rotational kinematic equation of motion and other equations of motion to solve these questions. The concept of centrifugal force is used in many applications and should be clear. Before proceeding in the calculations it is important to convert rpm (revolutions/minute) to radians/ second.