Question

A carrom board \[\left( {4ft \times 4ftsquare} \right)\] has the queen at the centre. The queen, hit by the strike moves to the front edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen
$\left( i \right)$ from the centre to the front edge
$\left( {ii} \right)$ from the front edge to the hole and
$\left( {iii} \right)$ from the centre of the hole

A. $\left( i \right)\dfrac{2}{3}\sqrt {10} ft\left( {ii} \right)\dfrac{4}{3}\sqrt {10} ft\left( {iii} \right)2\sqrt 2 ft$
B. $\left( i \right)\dfrac{4}{3}\sqrt {10} ft\left( {ii} \right)\dfrac{4}{3}\sqrt {10} ft\left( {iii} \right)2\sqrt 2 ft$
C. $\left( i \right)\dfrac{4}{3}\sqrt {10} ft\left( {ii} \right)\dfrac{2}{3}\sqrt {10} ft\left( {iii} \right)2\sqrt 2 ft$
D. $\left( i \right)\dfrac{2}{3}\sqrt {10} ft\left( {ii} \right)\dfrac{2}{3}\sqrt {10} ft\left( {iii} \right)2\sqrt 2 ft$

Answer 1

Hint: We can solve this problem with the concept of displacement. We also use vector and law of reflection for calculation. We know that displacement is the vector quantity hence in its calculation we have to use the vector concept. Displacement is the shortest distance from the initial to the final position of point. It is an overall change in the object positions.

Complete answer:
Displacement vector can be mathematically represented as follows:
       $s = {x_f} - {x_i} = \Delta x$
For the given question figure is given below,

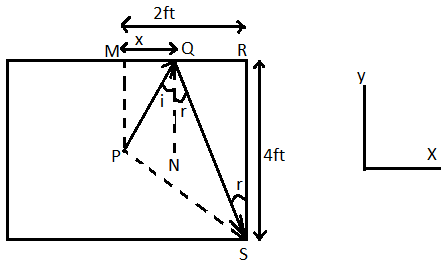
When a queen is hit by the striker from the centre it moves from $P$ to $Q$ then it rebounds and goes to the hole behind at $S$. Draw a perpendicular at $Q$, using law of reflection $\angle i = \angle r$and one at the point M.
By the law of reflection, $\angle i = \angle r$ (from triangle PQN and QRS)
$\dfrac{{2 - x}}{x} = \dfrac{4}{2}$

$\begin{gathered}
   \Rightarrow 4 - 2x = x \\
   \Rightarrow 3x = 2 \Rightarrow x = \dfrac{2}{3} \\
\end{gathered} $

Then $QR = \dfrac{4}{3}$
$(i)$ for displacement of queen from the centre to the front edge, $\overrightarrow {PQ} = \dfrac{{2\mathop i\limits^ \wedge }}{3} + 2\mathop i\limits^ \wedge $
Magnitude of the displacement $\left| {\overrightarrow {PQ} } \right| = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2} + {2^2}} = \dfrac{2}{3}\sqrt {10} ft$
$(ii)$for the displacement of queen from the front edge to the hole, $\overrightarrow {QS} = \dfrac{4}{3}\mathop i\limits^ \wedge + 4\mathop i\limits^ \wedge $
Magnitude of the displacement $\left| {\overrightarrow {QS} } \right| = \sqrt {{{\left( {\dfrac{4}{3}} \right)}^2} + {4^2}} = \dfrac{4}{3}\sqrt {10} ft$
$(iii)$for displacement of queen from the centre to the hole, $\overrightarrow {PS} = 2\mathop i\limits^ \wedge - 2\mathop j\limits^ \wedge $
Magnitude of the displacement $\left| {\overrightarrow {PS} } \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( 2 \right)}^2}} $$ = 2\sqrt 2 ft$

So, the correct answer is “Option A”.

Note:
We know that displacement is a vector quantity hence the direction of the displacement vector is always directed from the initial point to the final point. Displacement has both the distance and direction of the total motion along the straight path from the initial point to its final position. displacement is the relative position. For a particle which is in motion, for an instantaneous time velocity is the rate of the change of the displacement.