Question

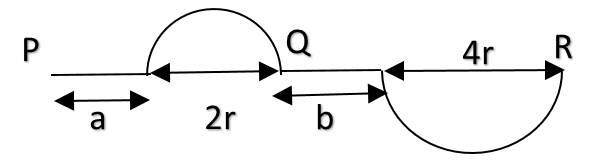
A car starts from point P and follows the path as shown in the figure and finally car stops at R.
Find the distance travelled and the displacement of the car if $a=7m, b=8m \ and \ r= \dfrac{11}{\pi}m?$

Answer 1

Hint: There are majorly two types of quantities, scalar and vector quantities. All the quantities are divided into these two categories. Scalar quantities are those quantities, which have only magnitude eg – mass, speed, pressure, etc. Vector quantities are those which have both magnitude and directions eg – weight, velocity and thrust. For instance, speed is a scalar quantity and velocity is a vector quantity.

Formula used:
Circumference of semi-circle = $\pi R$

Complete answer:
How do we measure distance?
Distance is a scalar quantity, hence can be measured by the scalar sum (normal sum) of individual distances.
Hence, distance = $a + \pi r + b + \pi\times (2r) = 3\pi r +a+b$
Hence total distance = $3\times \pi \times \dfrac{11}{\pi} + 7 + 8 = 33 + 15 = 48 m$

How do we measure displacement?
Displacement is a vector quantity, hence can be measured by the laws of vector addition. In general to get displacement, we just find the distance between initial and final point.
The distance between initial and final point = $a+2r+b+4r$
Displacement = $a+b+6r = 7+8+6\times \dfrac{11}{\pi} = 15 + \dfrac{66}{\dfrac{22}{7}} = 15 + 3\times 7 = 15 + 21 = 36 m$
Hence distance is 48 m and displacement is 36 m.

Note:
Displacement can be defined as the shortest distance between two points. Hence we can say that the displacement is the shortest distance between two points. Since both are indicating some lengths, hence both have S.I. unit ‘meter’. In the above question too, we can see that the displacement is less than distance. Displacement can either be negative, zero or positive. But distance is always positive for example, if a man starts to walk on a circular track, the net distance covered in 1 circle is $2\pi r$ whereas the displacement is zero as the starting and ending point is the same.