Question

A capillary tube made of glass of radius 0.15 mm is dipped vertically in a beaker filled with methylene iodide (surface tension = $0.05{\rm{ N}}{\rm{.}}{{\rm{m}}^{ - 1}}$, density = \[667{\rm{ kg}}{\rm{.}}{{\rm{m}}^{ - 3}}\]) which rises to height h in the tube. It is observed that the two tangents drawn from liquid-glass interfaces (from opp. sides of the capillary) make an angle of with one another. Then h is close to (g = $10{\rm{ m}}{{\rm{s}}^{ - 2}}$)
A. 0.172 m
B. 0.049 m
C. 0.087 m
D. 0.137 m

Answer 1

Hint:When a liquid is filled inside a capillary tube, that liquid rises into the capillary due to the surface tension of the liquid. This rise in the liquid into the capillary depends upon the density of the liquid, surface tension between the liquid and the capillary tube, radius of the capillary tube, and contact angle.

Formula used:
The formula to find the height in the capillary tube is,
\[h = \dfrac{{2T\cos \theta }}{{r\rho g}}\]
Where,
\[T\] is surface tension of methylene iodide
\[\theta \] is the angle of contact
\[r\] is radius of the capillary tube
\[\rho \] is density of methylene iodide
\[g\] is the acceleration due to gravity

Complete step by step solution:

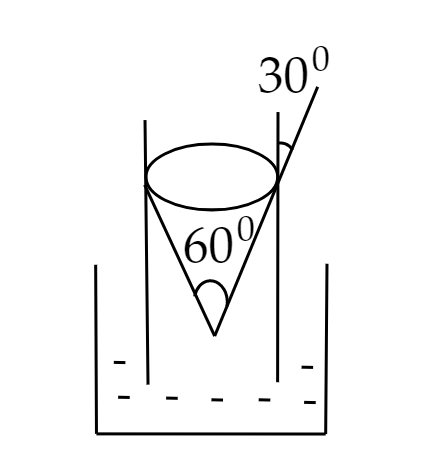
Image: A capillary tube dipped in a beaker filled with methylene iodide

Capillary tubes are very thin tubes made of a rigid material, such as plastic or glass in which a liquid flow up into the tubes against gravity in a process called capillary action (capillarity) and it will occur due to the cohesive force between the molecules of liquid and adhesive force between the surface of the tube and the liquid. The contact angle of liquid is defined as the angle it makes with the walls of the container and it depends both on the liquid as well as the container.

To find the height in the capillary tube we have,
\[h = \dfrac{{2T\cos \theta }}{{r\rho g}}\]
\[\Rightarrow h = \dfrac{{2 \times 0.05 \times \cos {{30}^0}}}{{0.15 \times {{10}^{ - 3}} \times 667 \times 10}}\]
\[\Rightarrow h = \dfrac{{2 \times 0.05 \times \left( {\dfrac{{\sqrt 3 }}{2}} \right)}}{{0.15 \times {{10}^{ - 2}} \times 667}}\]
\[\Rightarrow h = 0.0866\,m\]
\[ \therefore h \simeq 0.087m\]
Therefore, the closest value of h is 0.087 m.

Hence, Option A is the correct answer

Note: Due to the water molecules' attachment to the capillary tube's glass walls, water rises inside of it. The result of this adhesion and surface tension in the water is a phenomenon known as capillarity, which has a distinctive concave surface.