Question

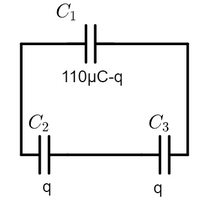
A capacitor of capacitance ${C_1} = 1\mu F$ charged upto a voltage \[V{\text{ }} = {\text{ }}110V\] is connected in parallel to the terminals of a circuit consisting of two uncharged capacitors connected in series and possessing capacitances ${C_2} = 2\mu F$ and ${C_3} = 3\mu F$. Then, the amount of charge that will flow through the connecting wires is:
A. $40\mu F$
B. $50\mu F$
C. $60\mu F$
D. $110\mu F$

Answer 1

Hint: Redistribution of charges occur due to potential difference and at equilibrium, The potential across AB would be constant (say $V$). We can find this common potential and then go for finding the charge transferred OR use $V = \dfrac{{{Q_1}}}{{{C_1}}} = \dfrac{{{Q_2}}}{{{C_2}}} + \dfrac{{{Q_3}}}{{{C_3}}}$

Complete step by step answer:
Consider the two capacitors in series to be initially discharged.
When a charged capacitor is connected to one or more uncharged capacitors (or in general even charged capacitors), The charge redistributes due to the voltage difference and after some time, they attain equilibrium when the voltage across common terminals become equal.

We are asked to find the amount of charge that flowed through the connecting wire.
This is equal to the amount of charge that the initially charged capacitor lost due to redistribution and also equal to the charge that the two capacitors together gained.

Let's find the total capacitance of the series connection. We know for parallel connection,
$\dfrac{1}{{{C_{eff}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \cdot \cdot \cdot + \dfrac{1}{{{C_n}}}$

So here,
${C_{eff}} = C'(say) = \dfrac{1}{{\dfrac{1}{2} + \dfrac{1}{3}}} = \dfrac{6}{5}\mu F$

Now, the total initial charge was :
${C_1}{V_1} = 1\mu F \times 110V = 110\mu C$

Now this charge redistributes among two capacitors: $C$ and $C'$as long as Their voltages become equal.
Let's say finally, the voltage across C and C' became $V$.
by conserving the initial charge :
$110\mu C = {C_1}V + C'V = V\left( {1\mu F + \dfrac{6}{5}\mu F} \right) = V\dfrac{{11}}{5}\mu F$
So we get $V = \dfrac{{5 \times 110\mu C}}{{11\mu F}} = 50V$

Now to find the charge that flowed, we can find the charge across $C'$ since both are the same.
So $q = C'V = \dfrac{6}{5}\mu F \times 50 = 60\mu C$

Note: Another simpler approach would be:
Assume the charge that flowed through the wire as $q$.
This flow stops when the potential becomes equal and at equilibrium, ${C_1}$ would have $110 - q$ $\mu C$ charge, and the two capacitors in series would have $q$ each.
Now since the potential is equal,
$\dfrac{{(110\mu C - q)}}{{{C_1}}} = \dfrac{q}{{{C_2}}} + \dfrac{q}{{{C_3}}}$
$\dfrac{{(110\mu C - q)}}{1} = \dfrac{q}{2} + \dfrac{q}{3}$
$110\mu C = q\dfrac{{11}}{6}$
$q = 60\mu C$