Question

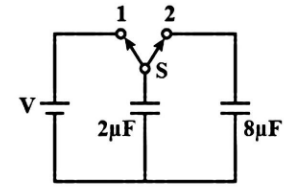
A capacitor of \[2\mu F\] is charged as shown in the diagram. When the switch \[S\] is turned to position \[2\] , the percentage of its stored energy dissipated is:

A. $0\% $
B. $20\% $
C. $75\% $
D. $80\% $

Answer 1

Hint: In order to solve this question first of all we will find the initial energy of capacitance and then find the final energy stored in the capacitor formula of energy stored in a capacitor. After that inorder to get the heat dissipated in the circuit we will find the difference between the final and initial energy.

Complete step by step answer:
Initially, the energy stored in \[2\mu F\] capacitor is
${U_i} = \dfrac{1}{2}C{V^2} \\
\Rightarrow {U_i} = \dfrac{1}{2}\left( {2 \times {{10}^{ - 6}}} \right){V^2} \\
\Rightarrow {U_i} = {V^2} \times {10^{ - 6}}J$
Initially, the charge stored in \[2\mu F\] capacitor is ${Q_i} = CV = \left( {2 \times {{10}^{ - 6}}} \right)V = 2V \times {10^{ - 6}}$ Coulomb. When switch $S$ Is turned to position 2, the charge flow and both the capacitors share charges till a common potential ${V_C}$ is reached.
${V_C} = \dfrac{{total\,charge}}{{total\,capacitance}} \\
\Rightarrow {V_C} = \dfrac{{2V \times {{10}^{ - 6}}}}{{\left( {2 + 8} \right) \times {{10}^{ - 6}}}}
\Rightarrow {V_C} = \dfrac{V}{5}volt \\ $
Therefore, finally the energy stored in both the capacitors is
${U_f} = \dfrac{1}{2}\left[ {\left( {2 + 8} \right) \times {{10}^{ - 6}}} \right]{\left( {\dfrac{V}{5}} \right)^2} \\
\Rightarrow {U_f}= \dfrac{{{V^2}}}{5} \times {10^{ - 6}}J \\ $
$\% $ Loss of energy, $\Delta U = \dfrac{{{U_i} - {U_f}}}{{{U_i}}} \times 100\% $
$\Delta U = \dfrac{{\left( {\dfrac{{{V^2} - {V^2}}}{5}} \right) \times {{10}^{ - 6}}}}{{{V^2} \times {{10}^{ - 6}}}} \times 100\% \\
\therefore \Delta U= 80\% $

Hence the correct option is D.

Note: One should take care that there is no flow of charge in open circuit, in order to maintain the flow of change closed circuit is must. When the switch is shifted from one position to another then there will be a change in the charge flowing path which will change the energy and hence there will be some heat loss.