Question

A capacitor is charged with a battery and energy stored is U. After connecting the battery another capacitor of the same capacity is connected in parallel with it. Then energy stored in each capacitor is:
$\begin{align}
  & A.\text{ }\dfrac{U}{2} \\
 & \text{B}\text{. }\dfrac{U}{4} \\
 & \text{C}\text{. 4U} \\
 & \text{D}\text{. 2U} \\
\end{align}$

Answer 1

Hint: In this question, we have two cases, where we need to find energy stored in a capacitor. In the first case, we have a capacitor connected to potential V. In the second case; same capacitor is connected to another capacitor in parallel. To find energy stored, using a formula of energy stored will give a relation between charge and capacitance (C). When capacitors are in parallel, charges are distributed equally hence charge on each capacitor will be $\dfrac{q}{2}$ calculate energy stored for each capacitor and get the value.

Complete step by step answer:

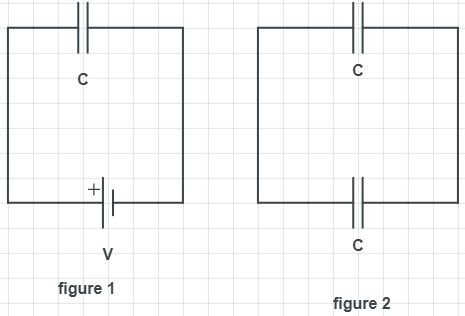
The question has stated that a capacitor is connected to a battery (V) and because of battery; energy is stored in a capacitor which is U. (shown in figure 1). Now this capacitor is connected to another capacitor having the same capacity in parallel connection. So we need to calculate how much energy is stored in each of the capacitors, shown in figure 2.
We know that energy stored in capacitor is given by,
 $U=\dfrac{1}{2}\dfrac{{{q}^{2}}}{c}......(1)$
Where q is charged stored in capacitor, C is capacitance of capacitor.
Now if you look at figure 2, charge stored on each of the capacitors is C. But initially capacitance of upper capacitor is C and capacitance of lower capacitor is zero. Finally charge from the upper capacitor distributes to the lower capacitor because potential is always the same in case of parallel combination, hence potential between these capacitors are also the same. So, charge on upper capacitor is $\dfrac{q}{2}$ and charge on lower capacitor is $\dfrac{q}{2}$ if U is the new energy stored in upper or lower capacitance, then
$\begin{align}
  & {{U}^{1}}=\dfrac{1}{2}\dfrac{{{\left( \dfrac{q}{2} \right)}^{2}}}{C} \\
 & =\dfrac{1}{2}\text{ }\dfrac{{{q}^{2}}}{4C} \\
 & {{U}^{1}}=\dfrac{1}{4}\text{ }\dfrac{1}{2}\dfrac{{{q}^{2}}}{C}=\dfrac{U}{4}\text{ }\left( from(1) \right) \\
\end{align}$
Hence energy stored in each capacitor is $\dfrac{U}{4}$.

So, the correct answer is “Option B”.

Note: When a capacitor is connected to battery, charge is stored. When a capacitor is charged, some work is done during the process of charging, which is stored in the form of electrostatic energy in the capacitor. Equation (1) is nothing but work stored in the form of electrostatic energy. Electrostatic force is conservative in nature.