Question

A capacitor has square plates each of side $l$ making an angle $a$ with each other as shown in the figure. Find the capacitance $C$ for a small value of $a$.

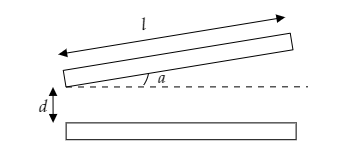
A) $\dfrac{{{\varepsilon _0}{l^2}}}{d}\left( {1 - \dfrac{{al}}{{2d}}} \right)$
B) $\dfrac{{{\varepsilon _0}{l^2}}}{{2d}}\left( {1 - \dfrac{{al}}{d}} \right)$
C) $\dfrac{{{\varepsilon _0}{l^2}}}{d}\left( {1 - \dfrac{{al}}{d}} \right)$
D) $\dfrac{{{\varepsilon _0}{l^2}}}{{2d}}\left( {1 - \dfrac{{al}}{d}} \right)$

Answer 1

Hint: The capacitance of a capacitor plate is found to be proportional to the area of the plate and inversely proportional to the distance between the plates. Here as one of the plates is inclined at some angle, the distance between the plates varies for the length of the plate. So we have to obtain an expression for the capacitance of a small element and then integrate this to obtain the capacitance of the entire capacitor.

Formula used:
The capacitance of a capacitor is given by, $C = \dfrac{{{\varepsilon _0}A}}{d}$ where ${\varepsilon _0}$ is the permittivity of free space, $A$ is the area of the plate and $d$ is the distance between the capacitor plates.

Complete step by step answer:
Step 1: Sketch a figure describing a small element of the capacitor plate and list its parameter.

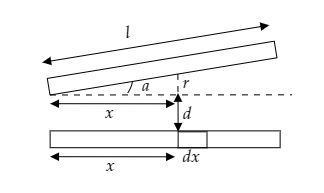
In the above figure, we considered a small element of an area $dA = ldx$ which is at a distance of $r + d$ from the other plate.
From trigonometric relations we have $r = x\tan a$ .
Thus the distance of separation becomes $d + x\tan a$ .
Step 2: Express the general relation for the capacitance of a capacitor to obtain the capacitance of the small element.
The general relation for the capacitance of a capacitor is given by, $C = \dfrac{{{\varepsilon _0}A}}{d}$ where ${\varepsilon _0}$ is the permittivity of free space, $A$ is the area of the plate and $d$ is the distance between the capacitor plates.
Based on the general relation we express the capacitance of the small element as $dC = \dfrac{{{\varepsilon _0}ldx}}{{d + x\tan a}}$.
For small values of $a$, $\tan a = a$ .
Then the capacitance of the small element will be $dC = \dfrac{{{\varepsilon _0}ldx}}{{d + xa}}$ or $dC = \dfrac{{{\varepsilon _0}ldx}}{{d\left( {1 + \dfrac{{xa}}{d}} \right)}}$ ------ (1)
Step 3: Integrate equation (1) to obtain the capacitance of the capacitor plate.
The integral of equation (1) is expressed as $C = \int\limits_0^L {dC} = \int\limits_0^L {\dfrac{{{\varepsilon _0}l}}{{d\left( {1 + \dfrac{{xa}}{d}} \right)}}dx} $ .
The above integral can be simplified as
$ \Rightarrow C = \dfrac{{{\varepsilon _0}l}}{d}\int\limits_0^L {{{\left( {1 + \dfrac{{xa}}{d}} \right)}^{ - 1}}dx} = \dfrac{{{\varepsilon _0}l}}{d}\int\limits_0^L {\left( {1 - \dfrac{{xa}}{d}} \right)dx} $ -------- (2)
We now split the integral for easier evaluation as
$ \Rightarrow C = \dfrac{{{\varepsilon _0}l}}{d}\int\limits_0^L {dx} - \dfrac{{{\varepsilon _0}la}}{{{d^2}}}\int\limits_0^L {xdx} $ .
Noe integrating the above integrals we get,
$ \Rightarrow C = \dfrac{{{\varepsilon _0}l}}{d}\left[ x \right]_0^l - \dfrac{{{\varepsilon _0}la}}{{{d^2}}}\left[ {\dfrac{{{x^2}}}{2}} \right]_0^l$ .
Applying the limits we get,
$ \Rightarrow C = \dfrac{{{\varepsilon _0}{l^2}}}{d} - \dfrac{{{\varepsilon _0}la}}{{{d^2}}}\left( {\dfrac{{{l^2}}}{2}} \right)$ .
$ \Rightarrow C = \dfrac{{{\varepsilon _0}{l^2}}}{d}\left( {1 - \dfrac{{a{l^2}}}{{2d}}} \right)$
Thus the capacitance is obtained as $C = \dfrac{{{\varepsilon _0}{l^2}}}{d}\left( {1 - \dfrac{{a{l^2}}}{{2d}}} \right)$ .

Therefore, the correct option is A.

Note:
Here the integration is done for the entire length of the capacitor and so the limits of integration range from $0$ to $l$ . The evaluation of integrals is always easier if we took all the independent constants out of the integral before evaluating the integral. To simplify the integral we applied binomial expansion as $a$ is mentioned to be small. By binomial expansion, ${\left( {1 + \dfrac{{xa}}{d}} \right)^{ - 1}} = \left( {1 - \dfrac{{xa}}{d}} \right)$ . This is substituted in equation (2).