Question

A cannon shell lands 2 km away from the cannon. A second shell, wired identically, breaks into two equal parts at the highest point. One part falls vertically. How far from the cannon will the other land?
A. 1 km
B. 3km
C. 4km
D. 5km

Answer 1

Hint: In order to solve the question, we will first of all we will find the velocity of shell 1 then by using conservation of momentum we will find the velocity of the shell 2 after that as mentioned in the question we will added up the distance covered by both shell 1 and shell 2.

Formula Used:
$MV = {M_1}{V_1} + {M_2}{V_2}$
M is the mass of cannon shell
V is the velocity of cannon shell
${M_1}$ is the mass of 1st part of shell
${V_1}$ is the velocity of 1st part of shell
${M_2}$ is the mass of 2nd part of shell
${V_2}$ is the velocity of 2nd part of shell

Complete step by step solution: 7
In the question we are given cannon shell lands 2 km away from the cannon. A second shell, wired identically, breaks into two equal parts at the highest point. One part falls vertically and we have to find far from the cannon will the other land

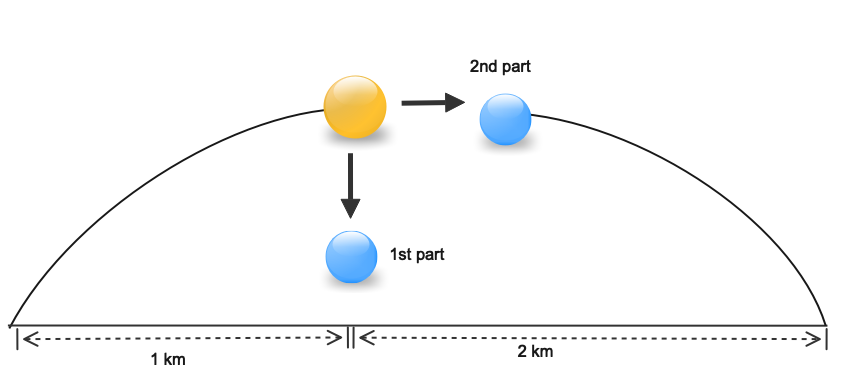
Distance covered by part 1 of the cannon shell
When the shell breaks, the first breaks at the highest point and one part falls vertically. At highest point velocity is zero and in question we are given the range as 2 km so the first part will fall at the distance of 1 km from the cannon
Hence distance covered by shell 1 is 1 km
Distance covered by part 2 of the cannon shell
Let V be the horizontal component of velocity of shell and let T be the total time of flight
V = horizontal component of velocity of shell
T = total time of flight
Now we will use the relation between velocity, distance and t
$V \times T = D$
D as given the question is 2 km hence the relation comes out
$V \times T = 2{\text{ km}}$
So the second other moves forward with the velocity V
Now we will conserve the momentum for the second part of the shell
Using the formula
$MV = {M_1}{V_1} + {M_2}{V_2}$
${V_1}$ is the velocity of 1st part of shell that is zero and ${V_2}$ is the velocity of 2nd part of shell which we have to find as shell broke in equal parts so ${M_1}$ is $\dfrac{M}{2}$ and ${M_2}$ is $\dfrac{M}{2}$
Substituting the values in the formula
$MV = \dfrac{M}{2}(0) + \dfrac{M}{2}{V_2}$
M will cancel and velocity of 2nd shell we gets
${V_2} = 2V$
Now by the relation between velocity, distance and time
$V \times T = D$
As it has coved half distance in half hence the time left is $\dfrac{T}{2}$
Substituting the values, we get distance covered by shell 2
$D = 2V \times \dfrac{T}{2}$
$D = V \times T$
Hence the value of $V \times T$ is 2 km as mentioned above
Now we will add the distance covered by both shells
1km + 2km
Therefore, the total distance is 3 km


Note:
Many of the people will not apply the conservation of moment in the second shell instead of that they may use the projectile motion formula but this way is easier method along with is many can mistake by not assuming the variable it is very important in this question as with that only we can solve all the formula.