Question

A candidate is required to answer $6$ out of $10$ questions which are divided into two groups each containing $5$ questions and he is not permitted to attempt more than $4$ from each group. In how many ways can he make up his choice?

Answer 1

Hint: This is a question based on combination concept. Let there be two sections (A and B) in the question paper and each section has $5$ different questions in it. So the candidate has to select some question from section A and some question from section B, and the total attempted question should be$6$. So we will make all cases of selecting questions and the total selected question should be six. For selecting questions we will use a combination concept.

Complete step-by-step answer:
Combination: If we have to select $r$ different things from total $n$ different things, total numbers of ways to select are –
${}^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!}$
Now, let us assume that the question paper has $2$ different sections, A and B, which has $5$ different questions each.

Now we have to select a total $6$ out of $10$ questions in the paper. So possible cases for this selection:

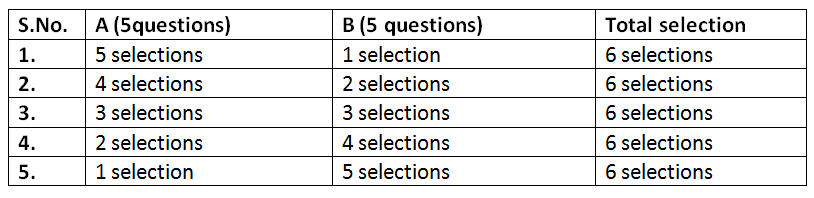
But the question has said that the candidate is not permitted to answer more than $4$ questions from each section, so we will reject case (1) and case (5), because in these cases we are selecting $5$ questions from one section.

So our favorable cases are:

Now we will calculate the number of ways for different cases.
(i) So for the first case, we have to select $4$ questions from section A and $2$ questions from section B. So number of ways of selecting $4$ questions out of $5$questions are ${}^{5}{{C}_{4}}$ and $2$ questions out of $5$ questions are${}^{5}{{C}_{2}}$. But these events are simultaneous, so total number of ways for case (1):
${}^{5}{{C}_{4}}\times {}^{5}{{C}_{2}}$
$\Rightarrow \dfrac{5!}{4!1!}\times \dfrac{5!}{3!2!}$
$\Rightarrow \dfrac{5}{1}\times \dfrac{5\times 4}{2}$
$\Rightarrow 5\times 10$
$\Rightarrow 50 $ways.

(ii) For the second case, we have to select $3$ questions from section A and section B each. So the number of ways of selecting $3$ questions out of $5$questions are${}^{5}{{C}_{3}}$. So, total number of ways for case (2):
${}^{5}{{C}_{3}}\times {}^{5}{{C}_{3}}$
$\Rightarrow \dfrac{5!}{3!2!}\times \dfrac{5!}{3!2!}$
$\Rightarrow \dfrac{5\times 4}{2}\times \dfrac{5\times 4}{2}$
$\Rightarrow 10\times 10$
$\Rightarrow 100$ways.

(iii) And for the second case, we have to select $2$ questions from section A and $4$questions from section B. So, total number of ways for case (3):
${}^{5}{{C}_{2}}\times {}^{5}{{C}_{4}}$
$\Rightarrow \dfrac{5!}{2!3!}\times \dfrac{5!}{4!1!}$
$\Rightarrow \dfrac{5\times 4}{2}\times 5$
$\Rightarrow 10\times 5$
$\Rightarrow 50$ ways.

So total number of ways for selecting total $6$ out of $10$questions are:
$=$ no. of ways for case (1) + no. of ways for case (2) + no. of ways for case (3)
$=$ $50$ways + $100$ways + $50$ways
$=200$ ways.

Note: (i) For this question, we have method-2 also. We have to select a total $6$ out of $10$questions but the condition is that we don’t have to select more than $4$questions from each section/group.
So, here we select $6$ out of $10$questions and then subtract the number of ways where we select $5$ questions from one of two different sections. So total numbers of ways are:
\[{}^{10}{{C}_{6}}-\left( {}^{2}{{C}_{1}}\times {}^{5}{{C}_{5}} \right)\times {}^{5}{{C}_{1}}\]
$\Rightarrow {}^{10}{{C}_{6}}-{}^{2}{{C}_{1}}\times {}^{5}{{C}_{5}}\times {}^{5}{{C}_{1}}$
$\Rightarrow \dfrac{10!}{6!4!}-\dfrac{2!}{1!1!}\times \dfrac{5!}{5!10!}\times \dfrac{5!}{1!4!}$
\[\Rightarrow \dfrac{10\times 9\times 8\times 7}{4\times 3\times 2\times 1}-2\times 1\times 5\]
\[\Rightarrow 10\times 3\times 7-10\]
$\Rightarrow 210-10$
$\Rightarrow 200 $ways.

(ii) In this question, students should take care of all cases carefully. Since calculations are a little tough, keep in mind that check all cases at least once at the end of the questions.