Question

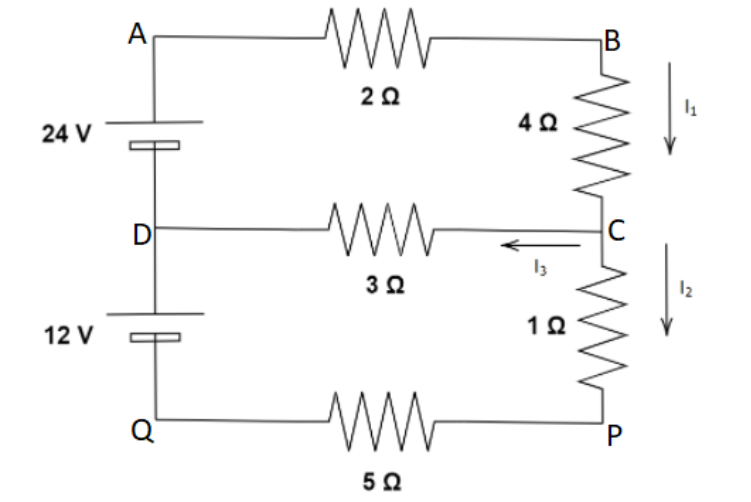
(A) Can the circuit shown in Figure be reduced to a single resistor connected to a battery? Explain. Calculate the currents
(B) \[{I_1}\]
(C) \[{I_2}\]
(D) \[{I_3}\]

Answer 1

Hint: We are asked to find three quantities of current in the figure by using Kirchhoff's laws. Initially we are asked if the given circuit can be reduced into one resistor and a battery. We can start by looking at the circuit and observing it will lead us to the solution to the first part of the question. Then we can solve for the three asked quantities using Kirchhoff’s laws.

Formulas used: Kirchhoff’s loop law states that the algebraic sum of potential difference, and resistive elements, in any loop must be equal to zero.

Complete step by step answer:
 We can start one by one.
(A) The given circuit cannot be converted into one resistor and a battery as there are already two voltage sources present (the two batteries).

(B) Applying Kirchhoff’s law
We can see that from the figure \[{I_1} = {I_2} + {I_3}\]

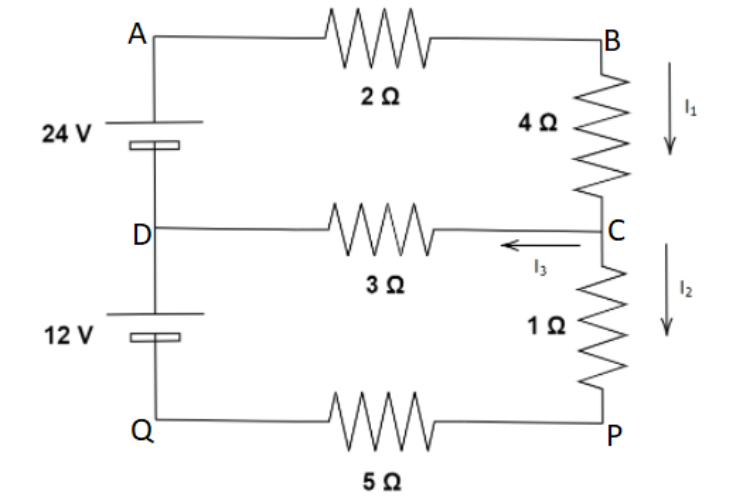
In the upper loop ABCD, we can apply Kirchhoff’s law and get,
\[24 = 2{I_1} + 4{I_1} + 3{I_3}\]
Then we can use the relation between all the three current and get,
\[3{I_3} + 2{I_2} = 8\]
We also divided the whole equation by three to get the above simpler equation.
Now applying the loop DCPQ, we get
\[12 = - 3{I_3} + {I_2} + 5{I_2}\]
We can simplify this in order to get,
\[4 = 2{I_2} - {I_3}\]

We can solve the final equations we got from solving the two loops using Kirchhoff’s loop rule and get,
\[{I_3} = 1A\]
\[\Rightarrow {I_2} = 2.5\,A\]
Now we have already seen that the relationships between the three values of current is given by
\[{I_1} = {I_2} + {I_3}\]
We now substitute the values in the above equation and get,
\[{I_1} = {I_2} + {I_3} \\
\Rightarrow {I_1} = 1 + 2.5 \\
\therefore {I_1} = 3.5\,A\]

In conclusion the values of the three unknown values of current is \[{I_1} = 3.5\,A\] , \[{I_3} = 1\,A\] , and, \[{I_2} = 2.5\,A\].

Note: Kirchhoff’s laws are usually used to analyze circuits. There are two, namely the current law and a voltage law. At every node, the sum of all current coming in the node must be zero. Nodes are places that attach to each other.