Question

A butler stole wine from a butt of sherry which contained \[32\% \] of spirit and then replaced it with wine containing only \[18\% \]. The butt was then of \[24\% \] only. How much of the butt had he stolen?

Answer 1

Hint: Here, we are required to find the total quantity of wine stolen from the butt by the butler. We will use the method of allegation to solve this question. We will find the fractional part of wine in each case given and then, after applying mixtures and allegations, we will find the final ratio which is stolen. The fractional part of wine from this ratio will be the required quantity which is actually stolen by the butler.

Formula Used:
By allegations, the required ratio is: \[h - d:d - l\] , where \[h\] is the higher strength, \[l\] is the lower strength and \[d\] is the desired strength.

Complete step-by-step answer:
Let the total liters present inside the butt be 100 liters.
Now, according to the question,
The butt of sherry contained \[32\% \] of spirit.
Hence, the quantity of spirit in the butt is \[32\% \] of 100 liters \[ = \dfrac{{32}}{{100}} \times 100 = 32\] liters
Also, the quantity of wine in the butt \[ = 100 - 32 = 68\] liters
Therefore, the ratio of Spirit and wine in the butt is \[32:68 = 8:17\]
In this, the wine is \[\dfrac{{17}}{{17 + 8}} = \dfrac{{17}}{{25}}\] of the total quantity………………………… \[\left( 1 \right)\]
Now, according to the question,
The butler replaced the stolen wine by the wine containing only \[18\% \] of spirit.
The amount of spirit in this 100 liter replaced wine is \[18\% \] of 100 liters \[ = \dfrac{{18}}{{100}} \times 100 = 18\]liters
Also, the quantity of wine in the replaced butt \[ = 100 - 18 = 82\]liters
Therefore, the ratio of Spirit and wine in the replaced butt is \[18:82 = 9:41\]
In this, the wine is \[\dfrac{{41}}{{41 + 9}} = \dfrac{{41}}{{50}}\] of the total quantity………………………… \[\left( 2 \right)\]
Now, it is given that the butt was then of \[24\% \] only
Similarly, the ratio of Spirit and wine is \[24:76 = 6:19\]
In this, the wine is \[\dfrac{{19}}{{19 + 6}} = \dfrac{{19}}{{25}}\] of the total quantity………………………… \[\left( 3 \right)\]
Now, to find the quantity of butt stolen by him, we will use the method of allegation.
Therefore, from \[\left( 1 \right)\], \[\left( 2 \right)\] and \[\left( 3 \right)\], here, \[l = \dfrac{{17}}{{25}}\] , \[h = \dfrac{{41}}{{50}}\] and \[d = \dfrac{{19}}{{25}}\],

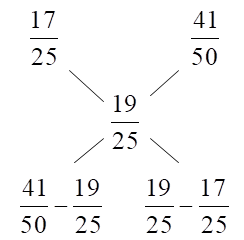
Hence, by the allegation method, we know that, \[h - d:d - l\]
 \[ \Rightarrow \dfrac{{41}}{{50}} - \dfrac{{19}}{{25}}:\dfrac{{19}}{{25}} - \dfrac{{17}}{{25}} = \dfrac{3}{{50}}:\dfrac{4}{{50}} = 3:4\] is the ratio of spirit and wine stolen.
Hence, the quantity of wine stolen from the butt \[ = \dfrac{4}{{4 + 3}} = \dfrac{4}{7}\]
Hence, \[{\dfrac{4}{7}^{{\rm{th}}}}\] of the wine from the butt has been stolen by the butler.

Note: An alternate way to solve this question is to apply the allegation method directly.
Now, we know that by allegations, the required ratio is: \[h - d:d - l\], where \[h\] is the higher strength, \[l\] is the lower strength and \[d\] is the desired strength.
Hence, directly substituting \[l = 18\] , \[h = 32\] and \[d = 24\], we get

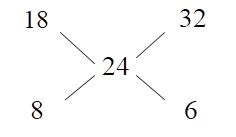
Hence, by the allegation method, we know that, \[h - d:d - l\]
 \[ \Rightarrow 32 - 24:24 - 18 = 8:6 = 4:3\] is the ratio of butt stolen to butt left.
Hence, the quantity of wine stolen from the butt \[ = \dfrac{4}{{4 + 3}} = \dfrac{4}{7}\]
Hence, \[{\dfrac{4}{7}^{{\rm{th}}}}\] of the wine from the butt has been stolen by the butler.