Question

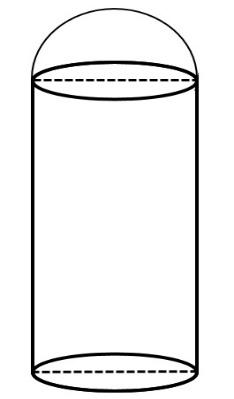
A building in the form of a cylinder surmounted by hemispherical dome. The base diameter of the dome is equal to $\dfrac{2}{3}$ of the total height of the building. Find the height of the building if it contains $67\dfrac{1}{21}{{m}^{3}}$ of air.

Answer 1

Hint: Here, take \[H\] as the height of the building such that \[H=h+r\] where is \[h\] is the height of the cylinder and r is the radius of cylinder and hemisphere. By the given data we have $d=2r=\dfrac{2}{3}(h+r)$. Find \[h\] in terms of $r$ and substitute in the formula $V=\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}}$, where $V$ is the volume of air in the building which is given as $67\dfrac{1}{21}{{m}^{3}}$. From the above equation we will get the value of r, then find h and substitute that value in \[H=h+r\] to find the height of the building.
Complete step by step answer:
We are given that a building in the form of a cylinder is surmounted by a hemispherical dome. The base diameter of the dome is equal to $\dfrac{2}{3}$ of the total height of the building. The volume of air in the building is $67\dfrac{1}{21}{{m}^{3}}$.
We have to find the height of the building.
Let \[H\] be the height of the building. Then, we can take \[h\] as the height of the cylinder and \[r\] as the radius of cylinder and hemisphere.
So we can write:
\[H=h+r\] …. (1)
Let the base diameter of the dome be $d$. Then we know that:
$d=2r$
We are given that the diameter $d$ is $\dfrac{2}{3}$ of the total height of the building. Hence, we will get:
$d=\dfrac{2}{3}H$
Since, $d=2r$ and \[H=h+r\] the above equation becomes:
$2r=\dfrac{2}{3}(h+r)$
By cross multiplication we get:
$\begin{align}
  & 3\times 2r=2(h+r) \\
 & 6r=2\times h+2\times r \\
 & 6r=2h+2r \\
\end{align}$
Now take, $2r$ to the left side, then $2r$ becomes $-2r$. Hence, our equation becomes:
$\begin{align}
  & 6r-2r=2h \\
 & 4r=2h \\
\end{align}$
Again, by cross multiplication we will get:
$\dfrac{4}{2}r=h$
Then, by cancellation we obtain:
$2r=h$
Now, we can write:
Total volume of air in the building = Volume of cylinder + Volume of hemisphere
Let the total volume of air in the building be V.
We know that:
Volume of cylinder = $\pi {{r}^{2}}h$
Volume of the hemisphere = $\dfrac{2}{3}\pi {{r}^{3}}$
Therefore, we can write:
$V=\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}}$
We are given that the total volume of air in the building, $V=67\dfrac{1}{21}{{m}^{3}}$
We also got that $h=2r$.Hence we will obtain:
$\begin{align}
  & 67\dfrac{1}{21}=\pi {{r}^{2}}\times 2r+\dfrac{2}{3}\pi {{r}^{3}} \\
 & \dfrac{67\times 21+1}{21}=2\pi {{r}^{3}}+\dfrac{2}{3}\pi {{r}^{3}} \\
 & \dfrac{1408}{21}=2\pi {{r}^{3}}+\dfrac{2}{3}\pi {{r}^{3}} \\
\end{align}$
Since, $2\pi {{r}^{3}}$ is the common factor, we can take it outside. Hence, we get:
$\dfrac{1408}{21}=2\pi {{r}^{3}}\left( 1+\dfrac{1}{3} \right)$
In the next step, by taking LCM we will obtain:
$\begin{align}
  & \dfrac{1408}{21}=2\pi {{r}^{3}}\left( \dfrac{3+1}{3} \right) \\
 & \dfrac{1408}{21}=2\pi {{r}^{3}}\times \dfrac{4}{3} \\
 & \dfrac{1408}{21}=\dfrac{8}{3}\pi {{r}^{3}} \\
\end{align}$
Now, by taking $\pi =\dfrac{22}{7}$ we will get:
$\dfrac{1408}{21}=\dfrac{8}{3}\times \dfrac{22}{7}\times {{r}^{3}}$
Next, by cross multiplication we obtain:
$\dfrac{1408\times 3\times 7}{21\times 8\times 22}={{r}^{3}}$
Next, by cancellation we will get:
$8={{r}^{3}}$
Now, by taking cube root on both the sides we get:
$\begin{align}
  & \sqrt[3]{3\backslash 8}=\sqrt[3]{{{r}^{3}}} \\
 & 2=r \\
\end{align}$
Hence, we got the radius as $r=2m$.
We have:
$\begin{align}
  & h=2r \\
 & h=2\times 2 \\
 & h=4 \\
\end{align}$
Hence, the height of the cylinder is $4m$.
We also have:
$\begin{align}
  & H=h+r \\
 & H=4+2 \\
 & H=6 \\
\end{align}$
Therefore, we can say that the height of the building is $6m$.

Note: Here, instead of finding $r$, you can also find $H$ directly by substituting $r$ in terms of $H$ from the equation $2r=\dfrac{2}{3}H$. Similarly you have to convert $h$ also in terms of $H$ and then substitute everything in the equation $V=\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}}$.