Question

A brick of mass m, tied to a rope, is being whirled in a vertical circle, with a uniform speed. The tension in the rope is:
A. The same throughout.
B. Largest when the brick is at the highest point of the circular path and smallest when it is at the lowest point.
C. Largest when the rope is horizontal and smaller it is vertical.
D. Largest when the brick is at the lowest point of the circular path and smallest when it is at the highest point.

Answer 1

Hint: When the brick is following a circular path in vertical direction then it is being acted by two forces, one due to the motion of the brick that is centrifugal force and other is due to the action of gravity that is the force of gravity. We will use this concept to find the tension at the smallest and highest point so that the relation between them can be established.

Complete step by step answer:
We know that the brick is acted by centrifugal force due to its circular motion with a uniform speed. We know that centrifugal force always acts away from the centre so we can write the expression for that centrifugal force as below:
\[F = mr{\omega ^2}\]
Here F is the centrifugal force, r is the distance between the centre of rotation and brick and \[\omega \] is the angular velocity of brick.
We are given that the motion of brick is in the vertical direction, that means we can say that force due to gravity is also acting on the body and its direction is vertically downward.
Let us consider downward direction as negative and upward direction as positive. We also know that tension due to brick in the rope will act towards the centre. We can draw the given condition as below:

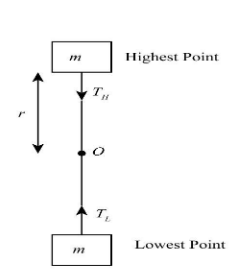
Using the concept of equilibrium and sign convention, we can write the expression for tension in the rope when the brick is at the highest point.
\[
\Rightarrow - {T_H} - mg + mr{\omega ^2} = 0\\
\Rightarrow{T_H} = mr{\omega ^2} - mg
\]……(1)
Here \[{T_H}\] is the tension in the rope at the highest point, and g is the acceleration due to gravity.

Similarly, we can write the expression for tension in the rope when the brick is at its lowest possible point.
\[
\Rightarrow{T_L} - mg - mr{\omega ^2} = 0\\
\Rightarrow{T_L} = mg + mr{\omega ^2}
\]……(2)
Here \[{T_L}\] is the tension in the rope at the lowest point.
Therefore, based on equation (1) and equation (2), we can say that tension at the lowest point is higher than the tension at the highest point, and option (D) is correct.

Note:We can take sign convention of forces acting on the rope as per our convenience that means we can consider downward direction as positive and upward direction as negative then also results will be same as obtained above.