Question

A boy and a man carry a uniform rod of length \[L\] , horizontally in such a way that the boy gets 1/4th load. If the boy is at one end of the road, the distance of the man from the other end is
A. $L/3$
B. $L/4$
C. $2L/3$
D. $3L/4$

Answer 1

Hint:To find the position of men, we must have knowledge of centre of mass. For now, we can understand it as a point on or outside the body where we can say the whole mass of the system is concentrated. In order to find the correct position of men we should be very much careful that, whole system should be in rotational equilibrium about the centre of mass of the rod. So, net torque about the centre of mass should be zero.
 $\sum \tau = 0$
 Here $\tau $ is torque.
Apply the conditions, you will get the answer

Complete step-by-step solution:

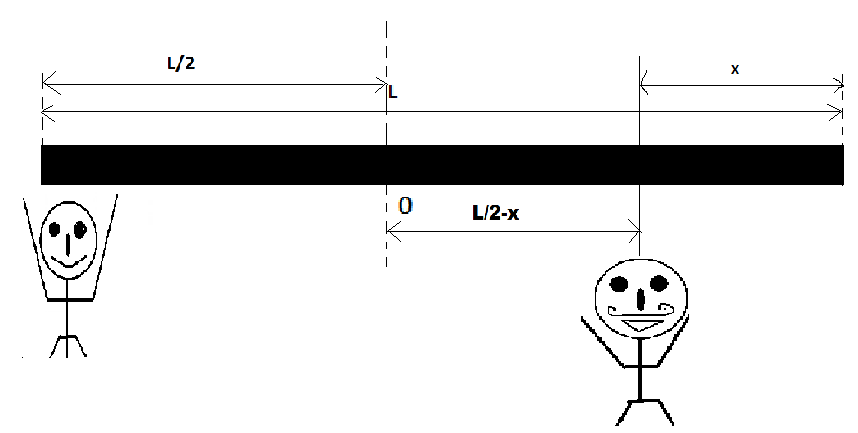
Since we already know, the rod is uniform so it’s centre of mass will be at L/2. According to the question , the boy is standing at the corner of one end and gets 1/4th weight of rod. We have to find the position of the man who gets the 3/4th weight of the rod from the other end. As we know this system should be rotational equilibrium so it is also quite expected that men will be on the other side of the centre of mass, at x distance from the other end. Refer the figure
So, let’s do it mathematically,
If the rod is in rotational equilibrium, net torque acting on it must be equal to zero. Keeping centre of mass as origin
 $\sum \tau = 0$
Here $\tau $ is torque.
We know torque = Force x perpendicular distance (from axis to point of action)
Both reaction forces tend to oppose each other’s rotational motion. Reaction force of the boy at left tends to rotate clockwise whereas the reaction force of the person at right is anticlockwise.
 $\dfrac{W}{4} \times \dfrac{L}{2} - \dfrac{{3W}}{4} \times \left( {\dfrac{L}{2} - x} \right) = 0$
On further solving,
 $
  \dfrac{W}{4} \times \dfrac{L}{2} = \dfrac{{3W}}{4} \times \left( {\dfrac{L}{2} - x} \right) \\
   \Rightarrow x = \dfrac{L}{3} \\
 $
Here,
L = Length of Rod
W= Weight of Rod



Note:- Always take care to check rotational equilibrium in such questions after applying all conditions as sometimes other constraints may not give you the proper result or may give several satisfying conditions. Formula to find centre of mass of a body is \[Xcm = \dfrac{{\sum\nolimits_{i = 1}^n {MiXi} }}{{\sum\nolimits_{i = 1}^n {Mi} }}\]
here,
 \[Mi = \]Mass of $i$ th part
 \[Xi = \] position of $i$ th particle from reference point.