Question

A body weighing $0.4\;kg$ is whirled in a vertical circle with a string making $2$ revolutions per second. If the radius of the circle is $1.2\;m$. Find the tension (a) at the top of the circle, (b) at the bottom of the circle. Given: $g = 10m{s^{ - 2}}$ and $\pi = 3.14$.

Answer 1

Hint: To solve this question, we first draw the free body diagram of the object at both top and the bottom positions. Then we equate the vertical forces to zero, because for the circle to stay in a constant radius the summation of the vertical forces must be zero.

Complete Step by step answer:

It is given in the question that,
Radius of the circle, $r = 1.2m$
The mass of the body is, $M = 0.4kg$
Therefore the weight of the body, $W = mg$
Taking the value of $g = 10m/{s^2}$
We have,
$W = 0.4 \times 10$
$ \Rightarrow W = 4N$
The angular velocity of the body is $2rps\;$
Converting rotations per second into radians per second,
$\omega = 2\pi \times 2$
$\omega = 4\pi rad/s$
Taking $\pi = 3.14$
$\omega = 4 \times 3.14$
$\omega = 12.56rad/s$
The centrifugal force is given by,
$F = mr{\omega ^2}$ directed away from the center of the circular path
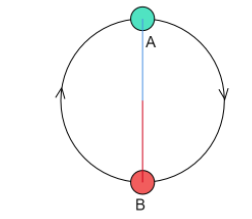
Let $A$ be the top position of the body,
Then the free body diagram of the body at $A$ will look like-

In the vertical direction, let the sum of forces be zero.
Then, we have the summation,
$T + mg = mr{\omega ^2}$
$ \Rightarrow T = mr{\omega ^2} - mg$
Putting the values,
$\Rightarrow$ $T = 0.4 \times 1.2 \times {\left( {12.56} \right)^2} - 4$
$T = 75.72 - 4$
$\Rightarrow$ $T = 71.72N$
Let $B$ be the bottom position of the body,
Then the free body diagram of the body looks like-

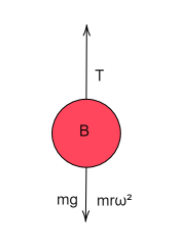
In the vertical direction, the forces balance each other,
Therefore they equate to-
$T = mg + mr{\omega ^2}$
Putting the values,
$\Rightarrow$ $T = 4 + 0.4 \times 1.2 \times {(12.56)^2}$
 $\Rightarrow$ $T = 75.72 + 4$
$T = 79.12N$
Thus the tension in the string when the object is positioned at the top of the circle is $71.72\;N$ and the tension when the object is at the bottom of the circle $79.12\;N$.

Note: In this scenario, the tension in the string is always directed towards the center of the circle and is considered as a centripetal force, as a reaction to this a centrifugal force equal to $mr{\omega ^2}$. Thus at the top, the tension is directed downwards and at the bottom, tension is directed towards the top.