Question

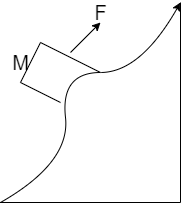
A body of mass M was slowly hauled up on a rough hill by a force F which at each point was directed along a tangent to the hill. Work done by the force
A. Is independent of the shape of trajectory
B. Depends upon the vertical component of displacement but is independent of horizontal component
C. Depends on both the components
D. Does not depends upon the coefficient of friction

Answer 1

Hint:-When two surfaces come in contact with each other or slide against each other, then a force is generated. This force is known as frictional force. This force tends to reduce or oppose the motion of the object.

Complete step-by-step solution:
Step I:
The frictional force is acting tangential to the path along the gravity and opposing the force. Therefore net work done by the force is given by the sum of work done by gravitational force and frictional force.
Step II:
Let $dS$ be an infinitely small area of the hill on which the body is placed. This small area can be considered as a plane. If the mass M makes an angle $\theta $ with the horizontal, then the force acting in upwards direction is the normal force N. The normal force is the force exerted on the body that is in contact with the hill. It’s formula is
$N = mg$
In Case of an inclined surface, the normal force is given by $N = mg\cos \theta $.
Step III:
The frictional force will act in an opposite direction to the movement of the block. If $\nu $ is the coefficient of friction then work done by frictional force is given by
${W_{friction}} = - \nu .N.dS$
$W = - \nu .mg\cos \theta .dS$
$W = - \nu .mg.(dS\cos \theta )$
$W = - \nu .mg.l$
Step IV:
Work done by gravitational force is given by
${W_{gravitation}} = - m.g.h$
Step V:
The frictional force depends only on the path followed by the object and not on the shape or size of the path. If ‘l' is the length of the bass of the hill and ‘h' is the height, then a work energy theorem will be used here.
According to the work energy theorem, the work done is equal to the difference in kinetic energies of the object.
$Work Done = {K_{initial}} - {K_{final}}$
Since the mass is hauled very slowly so kinetic energy is considered zero. Hence work done Will be
${W_{net}} + {W_{friction}} + {W_{gravitation}} = 0$
${W_{net}} = - \{ {W_{friction}} + {W_{gravitation}}\} $
$ = - \{ - \nu mgl - mgh)$
$ = \nu mgl + mgh$
Step VI:
Option A and C are the correct answer.

Note:- It is to be noted that the frictional force is affected by the angle and position of the object. If the object is pushed against the surface, then frictional force will increase and become more than the weight of the object. On the other hand, if the objects are just placed in contact with each other then the frictional force will be equal to the weight of the object.