Question

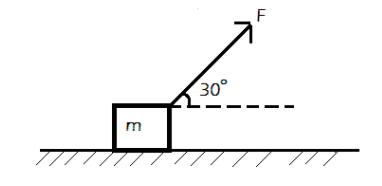
A body of mass \[m\] rests on a horizontal surface. The coefficient of friction between the body and the surface is\[\mu \]. If the body is pulled by a force \[F\]at an angle of \[{30^ \circ }\] with the horizontal and motion takes place, then contact force between two surfaces will be

$ \left( A \right)\mu mg \\
  \left( B \right)\mu \left( {mg - \dfrac{{\sqrt 3 }}{2}F} \right) \\
  \left( C \right)\mu \left( {mg - \dfrac{F}{2}} \right) \\
  \left( D \right)None\,of\,these \\ $

Answer 1

Hint: To solve this question, we are going to first analyze the figure and the information given in the question. Then, we’ll use the formula for the contact force of the two surfaces depending upon the coefficient of friction and the normal force and then find the normal force thus the contact force.

Formula used:
The contact force for the two surfaces is given by the formula,
\[{F_C} = \mu N\]
\[\mu \]is the coefficient of friction and \[N\]is the normal force.

Complete step by step solution:
It is given that the body of mass\[m\]is resting on a horizontal surface and the coefficient of friction is\[\mu \].
Force\[F\]is applied, which is having an angle equal to \[{30^ \circ }\]with the horizontal.
The contact force for the two surfaces is given by the formula,
\[{F_C} = \mu N\]
Now splitting the applied force into the vertical and the horizontal components, we get

The weight of the mass an the reaction force plus the vertical component of the applied force cancel out each other which can be expressed mathematically as:
\[F\sin {30^ \circ } + N = mg\]
Now, solving this for the value of the reaction force
\[N = mg - \dfrac{F}{2}\]
Thus, the contact force becomes
\[{F_C} = \mu \left( {mg - \dfrac{F}{2}} \right)\]
Hence, the correct answer is the option\[\left( C \right)\mu \left( {mg - \dfrac{F}{2}} \right)\].

Note: It is important to note that a contact force is any force that requires contact to occur. Contact forces are ubiquitous and are responsible for most visible interactions between macroscopic collections of matter. Pushing a car up a hill or kicking a ball across a room are some of the everyday examples where contact forces are at work.