Question

A body of mass $2kg$ initially at rest moves under the action of an applied horizontal force of $7N$ on a table with coefficient of kinetic friction = 0.1. Compute the
(a) work done by the applied force in $10s$.
(b) work done by friction in $10s$ ,
(c) work done by the net force on the body in $10s$ ,
(d) change in kinetic energy of the body in $10s$ ,
and interpret your results.

Answer 1

Hint: We will need to draw a diagram to understand the situation better. Then we will find the net force acting on the body. From this net force acting on the body, we will find the acceleration and from that, the distance moved by the body under the applied force. Net force acting on the body will be the difference between applied force and kinetic friction. Work done by a force is given as the dot product of force and distance moved by the body. Change in Kinetic energy can be found by using the final velocity and initial velocity of the body.
Formula used:]
 \[\begin{align}
  & {{F}_{frictional}}=\mu N \\
 & W=\overrightarrow{F}\cdot \overrightarrow{s} \\
 & s=ut+\dfrac{1}{2}a{{t}^{2}} \\
 & K.E=\dfrac{1}{2}m{{v}^{2}} \\
\end{align}\]

Complete answer:
First, we will illustrate the given situation in a diagram.

                          

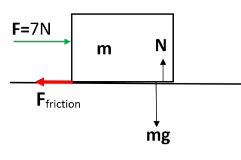
Now, frictional force will be given as,
\[{{F}_{frictional}}=\mu N\]
Where, \[\mu \] is the coefficient of kinetic friction.
               \[N\] is the reaction due to the weight of the body.

N is the normal reaction which is equal to weight of the body in magnitude. So,
\[N=mg=2\times 9.8=19.6N\] -- (here, we took g=9.8m/s)
Now, frictional force acting against the movement of the body will be
\[{{F}_{frictional}}=\mu N=0.1\times 19.6=1.96N\]

So, the net force acting on the body will be the difference between applied force and kinetic friction. I.e.

\[\begin{align}
  & {{F}_{net}}={{F}_{applied}}-{{F}_{frictional}} \\
 & {{F}_{net}}=7-1.96=5.04N \\
\end{align}\]

Therefore, the net force acting on the body is found to be \[5N\] . Now, we will find the acceleration of the body gained from this force.

We know, \[F=ma\] .

Then, \[a=\dfrac{F}{m}=\dfrac{5.04}{2}=2.52m/{{s}^{2}}\] .

Now, we will find the distance moved by the body due to the net force using the relation between acceleration and distance which is given by,

\[s=ut+\dfrac{1}{2}a{{t}^{2}}\]
But, initial velocity is zero in this case and time is taken as $10s$ in every case. So,
\[s=\dfrac{1}{2}a{{t}^{2}}=\dfrac{1}{2}\times 2.52\times {{\left( 10 \right)}^{2}}=126m\]
So, the distance moved by the body is \[126m\].

(a) Now, work done by the applied force in $10s$ can be found using the dot product between applied force and distance moved. i.e.
      \[W=\overrightarrow{F}\cdot \overrightarrow{s}=Fs\times \cos \left( \theta \right)\]
Here, applied force is $7N$ and distance moved is \[126m\].also, the angle between them is zero.
So, \[{{W}_{F}}=\overrightarrow{F}\cdot \overrightarrow{s}=Fs\times \cos \left( 0 \right)=7\times 126\times 1=882J\]
Therefore, work done by the applied force in $10s$ is found to be \[882J\].

(b) To find work done by friction in $10s$, we will use the same formula. But, force acting will be equal to \[1.96N\] and the angle between force and distance moved will be 180 degrees. The distance moved will be still the same.
So, \[{{W}_{f}}=\overrightarrow{F}\cdot \overrightarrow{s}=Fs\times \cos \left( 180 \right)=1.96\times 126\times -1=-246.96J\]

Therefore, work done by the frictional force in $10s$ is found to be \[-246.96J\].
(c) Now, to find work done by the net force on the body in $10s$, we will have to replace force with net force which is equal to \[5.04N\] and the angle between net force and distance moved by the body is zero.
So, \[{{W}_{{{F}_{net}}}}=\overrightarrow{F}\cdot \overrightarrow{s}=Fs\times \cos \left( 0 \right)=5.04\times 126\times 1=635.04J\]
Therefore, work done by the net force in $10s$ is found to be \[635.04J\] .

(d) To find change in kinetic energy, we need final velocity of the body. Final velocity can be found using the expression \[v=u+at\].
Here, the body is in rest initially and acceleration is already found. Time is given as $10s$.
So, final velocity is given as,
\[v=u+at=2.56\times 10=25.6m/s\]

Now, change in kinetic energy is given by,
\[\Delta K.E=\dfrac{1}{2}m{{v}^{2}}-\dfrac{1}{2}m{{u}^{2}}=\dfrac{1}{2}m\left( {{v}^{2}}-{{u}^{2}} \right)\]
We know initial velocity is zero. Then,
\[\Delta K.E=\dfrac{1}{2}m\left( {{v}^{2}}-{{u}^{2}} \right)=\dfrac{1}{2}\times 2\times {{\left( 25.2 \right)}^{2}}=635.04J\].
Therefore, a change in kinetic energy of the body in $10s$is found to be \[635.04J\].

So, we can conclude the answer as,
(a) Work done by the applied force in $10s$ is \[882J\] .
(b) Work done by friction in $10s$ is \[-246.96J\] .
(c) Work done by the net force on the body in $10s$ is \[635.04J\] .
(d) Change in kinetic energy of the body in $10s$ is \[635.04J\] .

Note:
We should know that the work done by frictional force is negative because frictional force is doing work against the motion of the body. We can also find the work done by net force just by adding the work done by applied force and work done by frictional force. Work done by net force and change in kinetic energy is found to be equal. Because, we know the work energy theorem which states that work done by a body is equal to change in kinetic energy.