Question

A body moves with a speed of 20 kmph in the first 5s and with a speed of 30 kmph in the next 5s. Then, the average speed of the body is:
(A) 25 kmph
(B) 24 kmph
(C) 0 kmph
(D) 10 kmph

Answer 1

Hint:-The given problem can be solved by taking the consideration of a body moving in a straight line with some speed for some time and then with another speed for the next given time. So, this question can be solved by taking the concept of average speed when a body travels with different speeds in different intervals.

Complete step-by-step solution:
Step 1:

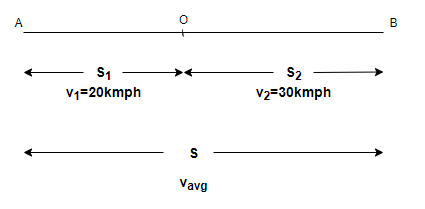
 As it is given in the question a body moves with a speed of 20kmph in the first 5s and with a speed of 30kmph in the next 5s.
So, average speed can be defined as – “When an object is moving with a variable speed, then the average speed of the object is the constant speed with which the object covers the same distance in a given time as it does while moving with variable speed during the given time. Average speed for the given motion is defined as the ratio of the total distance travelled by the object to the total time taken i.e.,
Average speed = Total distance travelled/ total time taken
Distance travelled can be calculated by – Distance travelled= given time x speed in that given time
Step 2: Distance travelled in first 5s with speed 20kmph i.e., \[\mathop S\nolimits_1 = \dfrac{5}{{3600}} \times 20\]
Distance travelled in next 5s with speed 30kmph i.e., \[\mathop S\nolimits_2 = \dfrac{5}{{3600}} \times 30\]
So, total distance travelled in 10s is given by \[S = \mathop S\nolimits_1 + \mathop S\nolimits_2 \]
So, from above equations total distance travelled can be calculated as
\[\Rightarrow S = \dfrac{5}{{3600}} \times 20 + \dfrac{5}{{3600}} \times 30\] on further solving this equation
\[\Rightarrow S = \dfrac{5}{{3600}} \times (20 + 30)\]
\[\Rightarrow S = \dfrac{5}{{3600}} \times 50\] ……………………….. (1)
And total time i.e., \[T = 10\]s which is equal to \[T = \dfrac{{10}}{{3600}}\]hrs ……... (2)
Step 3: So, we know that average speed i.e., \[\mathop v\nolimits_{avg} = \dfrac{S}{T}\] ………………………. (3)
So, by keeping the values from equation (1) and (2) into equation (3), we will get –
\[\Rightarrow \mathop v\nolimits_{avg} = \dfrac{5}{{3600}} \times 50 \times \dfrac{{3600}}{{10}}\] on further solving this equation
\[\Rightarrow \mathop v\nolimits_{avg} = \dfrac{5}{1} \times 50 \times \dfrac{1}{{10}}\]
\[\Rightarrow \mathop v\nolimits_{avg} = \dfrac{5}{{10}} \times 50\]
\[\Rightarrow \mathop v\nolimits_{avg} = 25\]kmph.
So, the average speed i.e., constant speed is 25kmph.

Note:-
An object is said to be moving with a variable speed if it covers equal distances in unequal intervals of time or unequal distances in equal intervals of time and these intervals can be small.
An object is said to be moving with uniform speed, if it covers equal distances in equal intervals of time and these intervals can be small.