Question

A body is revolving with a uniform speed `v’ in a circle of radius`$r$’. The tangential acceleration is:
A. $\dfrac{v}{r}$
B. $\dfrac{{{v}^{2}}}{r}$
C. $\dfrac{v}{{{r}^{2}}}$
D. zero

Answer 1

Hint: When a body moves in a circle then its motion is called circular motion. Now if it is moving with a constant speed then the motion is called uniform circular motion. Now it has two components of acceleration one is tangential while the other is centripetal which is always directed towards the centre.

Complete step by step solution:

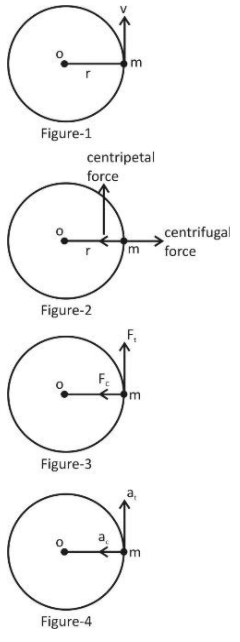
When a body is revolving around a circular path, it experiences two types of forces one is centripetal force and centrifugal force.

1. Centrifugal force describes the tendency of an object following a curved path to fly outwards away from the centre of the curve. It is not a real force but results from inertia (Inertia means the tendency of an object or a body to resist any change in its state of rest or motion).

2. Centripetal force is a real force that counteracts the centrifugal force and prevents the object from flying out, keeping it moving instead with uniform speed along the circular path.
(See figure-2)

3. There may be two forces ${{F}_{C}}$and ${{F}_{t}}$(Figure – 3) and its corresponding acceleration ${{a}_{C}}$and${{a}_{t}}$ (figure – 4).
Here,${{F}_{C}}=m{{a}_{C}}$
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}$
And, ${{F}_{t}}=m{{a}_{t}}$

4. Now, the tangential acceleration,
\[{{a}_{t}}=r\alpha \]
Where $\alpha $ is the angular acceleration of the particle.

5. The angular acceleration is defined as rate change of angular velocity $W$, so $\alpha =\dfrac{d\omega }{dt}$, but in uniform motion, $\omega =\dfrac{v}{r}$
(From figure – 1), here $V$ is constant because the particle is moving with uniform speed. Here $r$ is the radius of the circle which is fixed so, $\omega =$constant

6. Now, differencing the equation $\omega =$constant concerning time $t$ then\[\dfrac{d\omega }{dt}=\dfrac{d}{dt}\](constant)$\dfrac{d\omega }{dt}=0$($\because $differentiation of a constant is zero)

So, $\alpha =\dfrac{d\omega }{dt}=0$
So, ${{a}_{t}}=r\alpha =r\left( 0 \right)$
${{a}_{t}}=0$

Hence, the correct option is (D).

Additional information: When an observer is in the rotating frame then he feels a centrifugal force.

Note: The centripetal acceleration acts towards the centre of the circle into the particle whereas the centrifugal acceleration away from the centre.