
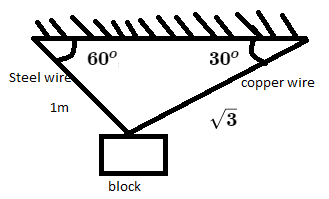
A block of weight

Answer
502.2k+ views
Hint: Here we apply the Hooke’s law for stress and strain to find the ratio
The Hooke’s law says that the displacement or scale of the deformation is directly proportional to the deforming force or load for relatively minor deformations of an object.
Hooke’s law also states that the strain of the material beyond the elastic boundary of that material is equal to the stress applied. The atoms and molecules contract as the elastic structures are strained before tension is added and they revert to their original state when the tension is withdrawn.
Complete step by step answer:
Given,
Young’s modulus for copper,
Young’s modulus for steel,
Length of copper wire,
Length of steel wire,
Elongation in copper wire is
Elongation in steel wire is
The angles subtended by copper and steel wires with ceiling are
The cross-sectional area
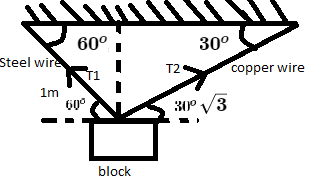
Let
Let
According to Hooke’s law
Stress =
Force
Also,
Force
Equation (i) divided by equation (ii), we get-
Now applying resultant of horizontal component
So, from equation (iii), we get-
Hence,
If elongation in copper wire is
Note:
Here we have to pay attention that the area is the same for both the wires, so the area gets cancelled. Also the horizontal component will be negative for steel wire.
The Hooke’s law says that the displacement or scale of the deformation is directly proportional to the deforming force or load for relatively minor deformations of an object.
Hooke’s law also states that the strain of the material beyond the elastic boundary of that material is equal to the stress applied. The atoms and molecules contract as the elastic structures are strained before tension is added and they revert to their original state when the tension is withdrawn.
Complete step by step answer:
Given,
Young’s modulus for copper,
Young’s modulus for steel,
Length of copper wire,
Length of steel wire,
Elongation in copper wire is
Elongation in steel wire is
The angles subtended by copper and steel wires with ceiling are
The cross-sectional area
Let
Let

According to Hooke’s law
Stress =
Force
Also,
Force
Equation (i) divided by equation (ii), we get-
Now applying resultant of horizontal component
So, from equation (iii), we get-
Hence,
If elongation in copper wire is
Note:
Here we have to pay attention that the area is the same for both the wires, so the area gets cancelled. Also the horizontal component will be negative for steel wire.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹ per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Which are the Top 10 Largest Countries of the World?

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Derive an expression for electric potential at point class 12 physics CBSE




