Question

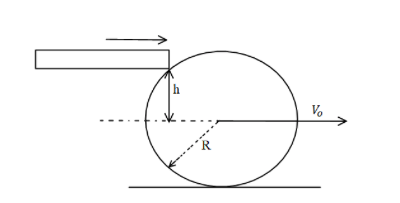
A billiard ball, initially at rest, is given a sharp impulse by cue. The cue is held horizontally at a distance h above the central line as shown in the figure. The ball leaves the cue with speed ${v_o}$. It rolls and slides while moving forward and eventually acquires a final speed $\left( {\dfrac{9}{7}} \right){v_o}$. If R is the radius of the ball, then h is,

A) $\dfrac{{2R}}{5}$.
B) $\dfrac{{3R}}{5}$.
C) $\dfrac{{4R}}{5}$.
D) $\dfrac{R}{5}$

Answer 1

Hint:Angular momentum is equivalent quantity to linear moment and it is conserved quantity. The total angular momentum of a body in a closed system is always conserved. Also the angular momentum can be expressed in terms of moment of inertia and angular momentum.

Formula used:The formula for angular momentum is given by $L = mvR$ where $m$ is mass $v$ is velocity and $R$ is the radius. Also the angular momentum can be expressed in terms of moment of inertia and angular velocity as $L = I{\omega _o}$.

Complete step by step answer:
As the angular momentum is conserved therefore the initial angular momentum is equal to final angular momentum.
${L_i} = {L_f}$
Here the moment of inertia is $I = \dfrac{2}{5}m{R^2}$ for the sphere. The change in angular momentum $\Delta L$ can be calculate as,
$ \Rightarrow \tau \Delta t = \Delta L$
$ \Rightarrow \tau \Delta t = I{\omega _o}$
$ \Rightarrow \tau \Delta t = \dfrac{2}{5}m{R^2}{\omega _o}$
Also the change in linear momentum is given by,
$ \Rightarrow F\Delta t = \Delta P$
$ \Rightarrow F\Delta t = m{v_o}$………eq. (1)
The initial angular velocity of the sphere is given by,
\[{\omega _i} = \dfrac{{{v_o}}}{R}\].
The final velocity of the sphere is given by,
$ \Rightarrow {\omega _i} = \dfrac{{\left( {\dfrac{9}{7}{v_o}} \right)}}{R}$
$ \Rightarrow {\omega _i} = \dfrac{{9{v_o}}}{{7R}}$
Since the angular momentum is conserved therefore,
${L_i} = {L_f}$
Let us calculate${L_i}$,
$ \Rightarrow {L_i} = I{\omega _o} + m{v_o}R$………eq. (2)
And the ${L_f}$ will be,
$ \Rightarrow {L_f} = I{\omega _f} + m{v_f}R$
$ \Rightarrow {L_f} = I\left( {\dfrac{{9{v_o}}}{{7R}}} \right) + mR\left( {\dfrac{{9{v_o}}}{{7R}}} \right)$………eq. (3)
As angular momentum is conserved ${L_i} = {L_f}$ therefore,
\[ \Rightarrow {L_i} = {L_f}\]
\[ \Rightarrow I{\omega _o} + m{v_o}R = I\left( {\dfrac{{9{v_o}}}{{7R}}} \right) + mR\left( {\dfrac{{9{v_o}}}{{7R}}} \right)\]
\[ \Rightarrow I{\omega _o} + m{v_o}R = \dfrac{{9{v_o}}}{{7R}}\left( {I + m{R^2}} \right)\]
\[ \Rightarrow \left( {\dfrac{2}{5}m{R^2}} \right) \cdot \left( {{\omega _o}} \right) + m{v_o}R = \dfrac{{9{v_o}}}{{7R}}\left( {\dfrac{2}{5}m{R^2} + m{R^2}} \right)\]
\[ \Rightarrow \left( {\dfrac{2}{5}m{R^2}} \right) \cdot \left( {{\omega _o}} \right) + m{v_o}R = \dfrac{{9{v_o}}}{{7R}}\left( {\dfrac{7}{5}m{R^2}} \right)\]
\[ \Rightarrow \left( {\dfrac{2}{5}} \right)m{R^2}{\omega _o} = \dfrac{{9{v_o}mR}}{5} - m{v_o}R\]
\[ \Rightarrow \left( {\dfrac{2}{5}} \right)m{R^2}{\omega _o} = \dfrac{{4m{v_o}R}}{5}\]
\[ \Rightarrow R{\omega _o} = 2{v_o}\]
\[ \Rightarrow {\omega _o} = \dfrac{{2{v_o}}}{R}\]………eq. (4)
We know that $\tau \Delta t = \dfrac{2}{5}m{R^2}{\omega _o}$ and also the torque is given by $\tau = {\text{force}} \times {\text{distance}}$ and the force applied on the sphere is at height h from the centre of the sphere therefore,
$ \Rightarrow \tau \Delta t = \dfrac{2}{5}m{R^2}{\omega _o}$
$ \Rightarrow F \cdot h \cdot \Delta t = \dfrac{2}{5}m{R^2}{\omega _o}$………eq. (5)
Dividing equation 5 with equation 1.
$ \Rightarrow \dfrac{{F \cdot h \cdot \Delta t}}{{F\Delta t}} = \dfrac{{\dfrac{2}{5}m{R^2}{\omega _o}}}{{m{v_o}}}$
$ \Rightarrow h = \left( {\dfrac{2}{5}} \right) \cdot \left( {\dfrac{{{\omega _o}{R^2}}}{{{v_o}}}} \right)$………eq. (6)
Replace the value of ${\omega _o}$ from equation (4) to equation (6).
$ \Rightarrow h = \left( {\dfrac{2}{5}} \right) \cdot \left( {\dfrac{{{\omega _o}{R^2}}}{{{v_o}}}} \right)$
Replace ${\omega _o} = \dfrac{{2{v_o}}}{R}$ in the above relation.
$ \Rightarrow h = \left( {\dfrac{2}{5}} \right) \cdot \left( {\dfrac{{{\omega _o}{R^2}}}{{{v_o}}}} \right)$
$ \Rightarrow h = \left( {\dfrac{2}{5}} \right) \cdot \dfrac{{{\omega _o}{R^2}}}{{{v_o}}}$
$ \Rightarrow h = \left( {\dfrac{2}{5}} \right) \cdot \left( {\dfrac{{{R^2}}}{{{v_o}}}} \right) \cdot \left( {\dfrac{{2{v_o}}}{R}} \right)$
$ \Rightarrow h = \dfrac{{4R}}{5}$

So the correct answer for this problem is option C.

Note:Students should remember the concept and formula of angular momentum as it helps in solving these types of problem in which rotational motion is involved. Also it is advisable for students to remember the moment of inertia of some standard shapes as it is extremely important for students to remember the moment of inertia of the standard shapes because it is important for solving the problem.