Question

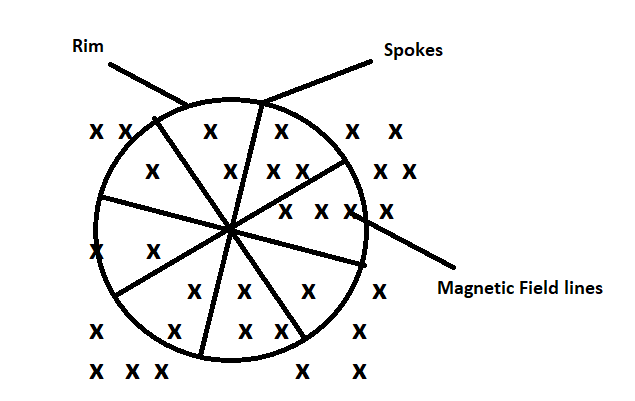
A bicycle wheel of radius \[0.5{\rm{ }}m\]has \[32\] spokes. It is rotating at the rate of \[120\]revolutions per minute, horizontal component of earth of earth’s magnetic field ${\beta _H} = 4 \times {10^{ - 5}}T$. The emf induced between the rim and the centre of wheel will be:

A.$6.28 \times {10^{ - 5}}V$
B.$4.8 \times {10^{ - 5}}V$
C.$6 \times {10^{ - 5}}V$
D.$1.6 \times {10^{ - 5}}V$

Answer 1

Hint: An electromotive force, is the electrical action produced by a non-electrical source. Hence emf is directly proportional to magnetic field, area swept by spoke and revolutions made by wheel per second.

Complete Step by step answer: Radius = \[r{\rm{ }} = {\rm{ }}0.5{\rm{ }}m\]
Earth’s magnetic field ${\beta _H} = 4 \times {10^{ - 5}}T$.
Number of spokes = \[n{\rm{ }} = {\rm{ }}32\]
Number of rotations completed per minutes by wheel \[ = {\rm{ }}120\]
Hence rotations completed per second by a wheel = $\dfrac{{120}}{{60}} = 2$ revolutions per second.
Since radius of the wheel is \[0.5m\], the length of each spoke = \[0.5m\]
The rate of change of an angle with respect to velocity is called angular velocity. The SI unit of angular velocity id radian per second.
Hence angular velocity = $w = 2\pi n$
In time period of $T$the area swept by one spoke = $\pi {r^2}$
The time period of $T$the area swept by one spoke = $\pi \times {(0.5)^2}$= $0.25\pi {m^2}$
The emf induced in the $e = \dfrac{{d\phi }}{{dt}}$
The emf induced in the $e = \dfrac{{d(BA)}}{{dt}}$………………………………………………………….. (I)
Where $B$= magnetic field and
$A$= surface area
We can write equation (I) as $e = \dfrac{{BA}}{T}$………………………………………………………. (II)
Since the frequency is the number of occurrences of a repeating event per unit of time,
$T = \dfrac{1}{f}$
\[\Rightarrow f = \dfrac{w}{{2\pi }}\]
$\Rightarrow f = \dfrac{{4\pi }}{{2\pi }}$
$\Rightarrow f = 2Hz$
Now, we can write equation (II) as:
\[e{\rm{ }} = {\rm{ }}BAf\]
Means emf is directly proportional to magnetic field, area swept by spoke and revolutions made by wheel per second.
$\Rightarrow e = 4 \times {10^{ - 5}} \times 0.25\pi \times 2$
$\Rightarrow e = 6.28 \times {10^{ - 5}}V$

Therefore the emf induced between the rim and the centre of the wheel will be = $e = 6.28 \times {10^{ - 5}}V$. So, the correct option is A.

Note: E.M.F always opposes the change in magnetic flux associated with a conducting loop. Depending on the direction of the induced current it can be signed negative or positive.