Question

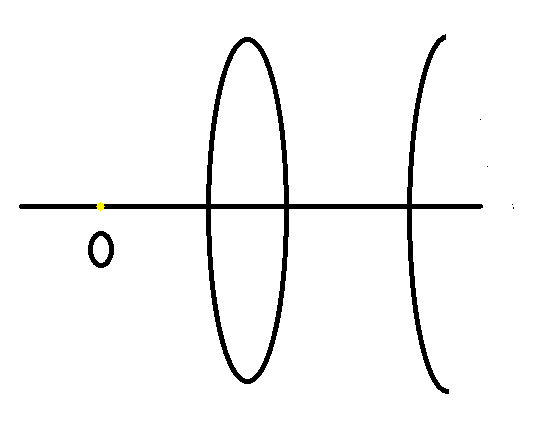
A biconvex lens, \[{f_1} = 20cm\], is placed $5cm$ in front of a convex mirror, \[{f_2} = 15cm\]. An object of length 0f $2cm$ is placed at a distance $10cm$ from the lens. If overall magnification is $\dfrac{X}{3}$. Then find out the value of $X$?

Answer 1

Hint: Here we will be using lens formula to solve this problem. And also apply the Cartesian sign convention of lens and mirror.

Formula used:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Linear magnification is given by${\text{ }}m = \dfrac{v}{u}$
Total magnification, $m = {m_1} \times {m_2} \times {m_3}$
Where $f$ is the focal length, $v$ is image distance, $u$ is object distance.
Here we will be using the lens formula to solve this problem. And also apply the Cartesian sign convention of lens and mirror.

Complete step by step answer:
Let, ${f_1}$ be the focal length of the bi-convex lens and ${f_2}$ be the focal length of the convex mirror. Then an object of length $2cm$ is placed at a distance $10cm$ from the lens. Let ‘$m$’ be the linear magnification.
$ \Rightarrow {f_2} = + 15cm$
${f_1} = + 20cm$, $h = 2cm$, $u = - 10cm$ (use Cartesian sign convention)
Overall magnification is $\dfrac{X}{3}$.
We have to find the value of $X$.

Case 1:
From lens formula,
\[ \Rightarrow \dfrac{1}{{20}} = \dfrac{1}{v} - \dfrac{1}{{ - 10}}\]
$ \Rightarrow v = - 20cm$
Therefore, magnification of first image,
${m_1} = \dfrac{v}{u}$
$ \Rightarrow m_1= \dfrac{{ - 20}}{{ - 10}}$
 $ \Rightarrow m_1=+ 2$
From this we can say that, image obtained is real.

Case 2:
Now, the first image will act as the object for a convex mirror. Therefore, object distance for the mirror is
$ \Rightarrow u' = \left( {20 + 5} \right)$
$ \Rightarrow 25cm$
From the lens formula,
$ \Rightarrow \dfrac{1}{{{f_2}}} = \dfrac{1}{{v'}} - \dfrac{1}{{u'}}$
$ \Rightarrow \dfrac{1}{{15}} = \dfrac{1}{{v'}} - \dfrac{1}{{25}}$
$ \Rightarrow v' = \dfrac{{75}}{8}cm$ .
Therefore second magnification will be,
$ \Rightarrow {m_2} = \dfrac{{v'}}{{u'}}$
 $ \Rightarrow \dfrac{3}{8}$
Now, the second image acts as an object for the lens.
Then, $ \Rightarrow u'' = \dfrac{{75}}{8} + 5$
 $ \Rightarrow \dfrac{{115}}{8}cm$
From lens formula,
$ \Rightarrow \dfrac{1}{{v''}} - \dfrac{1}{{\left( {\dfrac{{115}}{8}} \right)}}$
$ \Rightarrow \dfrac{1}{{ - 20}}$
$ \Rightarrow {v^{''}} = \dfrac{{460}}{9}cm$
Thus, final magnification,
$ \Rightarrow {m_3} = \dfrac{{{v^{''}}}}{{{u^{''}}}}$
$ \Rightarrow \dfrac{{32}}{9}$
Therefore, overall magnification will be, $m = {m_1} \times {m_2} \times {m_3}$
$ \Rightarrow m = 2 \times \dfrac{3}{8} \times \dfrac{{32}}{9}$
$ \Rightarrow \dfrac{8}{3}$ …………. (1)
Hence, given in the question, $m = \dfrac{X}{3}$ ……………. (2)
On comparing (1) and (2), we get
$X = 8$.

$\therefore$ The value of $X=8$.

Additional information:
All distances are measured from the pole of the mirror and along the principal axis.
The distances measured in the direction of the incident light are taken as positive while those measured in the direction opposite to the incident light are taken as negative.

Note:
All distances are measured from the optic center of the lens and along the principal axis.
The distances measured in the direction of the incident light are taken as positive while those measured in the direction opposite to the incident light are taken as negative.